이 글의 큰 주제이기도 한 ‘데이터로 구동하는 시스템 제어—이론과 응용의 새로운 전개와 최신 동향—’에 대해서, 총론의 목적은 데이터 구동 제어의 지금까지 흐름과 최근 동향에 대해서 간단히 해설하는 것이다.
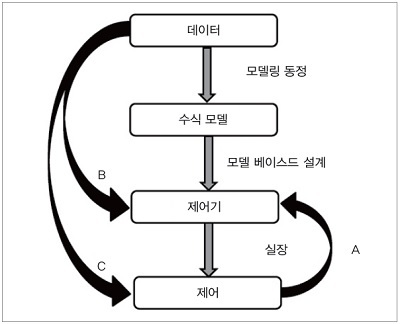
우선 데이터 구동 제어의 아웃라인을 그림 1에 나타냈다. 제어계를 설계하기 위해서는 시스템 동정 등에 의해 대상의 동특성 법칙을 나타내는 수식 모델을 작성하고, 그것에 근거한 설계를 추진하는 것이 통상의 합리적인 수단이다. 이것이 그림 1에서 보면 중심의 세로 화살표의 흐름이다. 한편 그림 1에서 대상의 수식 모델을 거치지 않고 데이터를 직접 이용함으로써 제어계를 갱신하거나(그림 1에서 A), 데이터에 직접 근거해 설계하는(그림 1에서 B나 C) 접근법이 활발히 연구되고 있다. 이들이 이른바 데이터 구동 제어라고 불리는 접근법이다.
최근 몇 년간 데이터 구동 제어에 관한 많은 연구 성과가 발표되고 여러 학회의 해설 기사나 논문 특집호에서도 많이 다루고 있으며, 국제회의에서도 관련된 OS 기획이나 강연이 활발하게 이루어지고 있다. 예를 들면 2023년 7월에 일본 요코하마에서 개최된 IFAC World Congress에서도 매우 많은 관련 세션이 편성되어 데이터 구동 제어에 관련된 많은 최신 연구 성과를 청강할 수 있었다. 이와 같이 최근 몇 년 사이 급속히 데이터 구동 제어는 제어계 설계의 한 분야로서 확립되어 가고 있다고 할 수 있다.
한편으로 이러한 학제적인 움직임과 함께, 예를 들면 실제 응용으로서는 의료복지나 건설기계 등의 응용에서 유용성을 나타낸 실제 응용 예도 볼 수 있게 됐다. 또한 데이터 구동 제어를 기간 기술의 하나로서 도입하기 위해 기업 교육에 포함시키려고 하는 움직임도 있다.
이 데이터 구동 제어의 발전 동기에는 우선은 모델에 근거한 제어의 접근법으로는 대응할 수 없는 경우, 즉 모델을 구하는 것이 어떠한 이유로 매우 곤란한 경우에 대응하기 위한 필요성을 들 수 있다. 이 곤란함의 이유에도 본질적으로 동특성이 너무 복잡해서 동정을 하는 것이 곤란하다고 하는 이유에서부터 이상적인 동정 실험을 하는 것이 코스트·시간·인적 자원의 관계로 어렵다, 또한 장치의 안전상 PE성이 높은 이상적인 동정 입력을 인가할 수 없다 등과 같은 다양한 이유를 들 수 있다. 어쨌든 동정을 하는 것이 어려운 경우에 하나의 돌파구나 활로의 입장으로서 데이터 구동 제어가 발전해 온 측면이 있다. 이에 더해 데이터가 갖고 있는 정보를 수식 모델에 압축하지 않고 그대로 제어계 설계에 반영시키고 싶다는 동기도 들 수 있다.
여기에는 모델화에는 데이터가 불충분한 경우라도 목표로 하는 제어계 설계에 활용할 필요가 있는 상황의 대응도 포함된다. 이러한 예로는 리아프노프(Lyapunov) 방정식을 이용해 안정인가 아닌가를 조사하고 싶을 때, 모델화를 거치지 않고 데이터로부터 리아프노프 방정식을 풀어 안정성을 해석하는 방법도 제안되어 그것에 의해 대규모 네트워크계 제어의 입력 노드를 결정하는 문제에 응용하는 등 흥미로운 전개도 볼 수 있다. 이와 같이 데이터를 직접적으로 제어계 설계에 활용함으로써 새로운 방법이나 발견의 기대라는 점도 동기의 하나로 생각할 수 있다.
이러한 배경 아래, 구동 제어에 관련된 최신 연구 동향과 앞으로의 발전으로 이어질 연구의 주제, 그리고 실제 응용에서 발휘된 데이터 구동 제어의 적용 사례 등을 다루어 보려고 한다. 이를 위한 도입으로서 이 글에서는 이 데이터 구동 제어의 지금까지의 흐름과 최신 연구 동향에 대해 간결하게 해설한다.
여기서는 하나의 분류 예로서 그림 1에 나타낸 오른쪽 화살표 A와 같이 노미널 모델이나 사전 정보 등으로부터 어떠한 제어기가 설계되어 있고, 그 후에 제어기의 성능을 유지·갱신한다고 하는 접근법과 왼쪽 화살표 B나 C와 같이 모델을 거치지 않고 데이터에 직접 근거한 설계의 접근법으로 나눠서 해설한다.
데이터를 직접 이용한 제어기 갱신·조정
데이터를 직접 이용한 제어라는 점에서, 특히 갱신이나 조정이라는 관점에서 흐름을 살펴보기로 하자. 전형적인 세팅으로서 그림 2와 같은 피드백 루프계를 생각한다. 가장 오래된 것은 PID 제어기의 갱신으로 잘 알려진 지글러 니콜라스법(Ziegler-Nichols Method)이나 한계감도법일 것이다. 전자는 얻은 스텝 응답 데이터의 기울기나 지연으로부터 미리 만들어진 대응표를 기초로 C의 파라미터를 결정하는 방법이며, 후자는 발산 직전의 응답이 될 때까지 제어기를 하이 게인화함으로써 그때의 진동 주기와 게인으로부터 파라미터를 결정하는 방법이다. 이와 같이 데이터를 직접 갖고 있는 제어기 갱신법이지만, 거기에는 설계자·사용자의 정성적 지표나 주관적 방침이 포함되어 있으며, 그 방법도 몇 번이나 반복해서 하는 것으로 되어 있다.
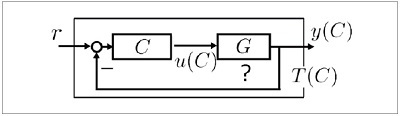
이러한 문제에 대해서 주어진 목표 응답과의 제곱 오차를 최소화하는 것으로 응답 성능의 향상이라는 목표를 순수하게 표현해 최적화하는 방법이 Iterative Feedback Tuning(IFT)으로 제안되어 있다. 제어 목표를 그대로 실현한 가장 순수한 데이터 구동 제어기 갱신법이지만, 유일한 결점으로 비선형 최적화를 실행할 때에 필요한 여러 번의 실험을 들 수 있다. 단, 순수하기 때문에 수렴성이나 안정성 등 많은 이론 해석이나 응용 예도 보고되어 있다. IFT의 개념을 다입출력계로 확장한 방법의 하나로서 비대각 요소의 간섭 저감화에 주목한 Correlation based Tuning(CbT)도 제안되어 있다.
그런데 IFT에서 여러 번의 실험을 피하는 방법으로서 2000년대 초반에 Virtual Reference Feedback Tuning(VRFT)과 Fictitious Reference Iterartive Tuning(FRIT)이 각각 독립적으로 제안됐다. 양쪽 모두 탁상 위의 가상적인 폐루프계를 도입함으로써 최초의 1회 실험 데이터로 소망(에 가까운)하는 제어기로 갱신을 획득하고 있다는 점에서 비슷하기는 하지만, VRFT가 개루프계, FRIT가 폐루프계를 최적화하고 있다는 본질적 차이점을 비롯해 최적성을 보증하는 프리 필터도 VRFT는 중역 특성을, FRIT는 저역 특성을 강조하고 PID 제어기에 대해서는 전자는 최소제곱법으로 가능한 한편, 후자는 비선형 최적화를 요구하는 등 몇 가지 차이점도 있다. 따라서 각각의 특징을 반영한 상황이나 목적에 따라 구분해서 사용하면 된다고 생각된다.
제어 사양을 목표 응답에 대한 추종 성능 향상으로 하면 통상의 선형 시불변 시스템에 관한 방법론으로서는 확립되어 있으며, VRFT는 가상 참조 신호와 프리 필터의 생성, FRIT는 의사 참조 신호의 생성만 가능하면 어떠한 제어계에서도 적용은 가능하다. 다입출력계에 대해서도 알고리즘 표기의 번잡함이나 최적화의 계산기 부하 문제에 주목하면, 동일한 이론적 보증 아래에서 적용할 수 있다. 또한 프로세스 제어계 등에서 피해야 할 과대한 입력을 고려한 E-FRIT도 제안되어 실용 예가 보고되어 있다.
이들은 2000년~2010년대 전반에 제안된 방법인데, 최근에 제안된 새로운 기법을 몇 가지 소개한다. 우선, 상황을 2자유도 제어계로 한정한 경우의 방법으로서 응답 특성만을 개선하는 것이라면 피드포워드 제어기를 수정하면 된다는 사실에 입각한 Estimated Reponse Iterative Tuning(ERIT)이 제안되어 있다. 이것은 피드백 제어기 부분을 바꾸지 않으면 피드포워드 제어기를 변경한 후의 응답을 초기 데이터와 제어기만으로 표현할 수 있다는 사실을 이용해, 이 변경 후의 응답이 목표 응답이 되도록 피드포워드 제어기를 구하는 것이다.
그런데 이 개념 자체를 통상의 1자유도 제어계에 그대로 적용하면, 아무래도 대상의 모델 G가 평가함수에 포함되어 버린다. 그래서 내부 모델 제어의 개념을 이용해 G를 목표 응답 모델 Td와 그것을 실현하는 이상적 제어기 Cd로 표현함으로써 대상 모델을 없애고 결과적으로 이미 알려진 정보만으로 목표 응답을 실현하는 제어기를 구하는 Virtual Internal Model Tuning(VIMT)이 제안되어 몇 가지 확장이 이루어져 있다.
또한 VRFT에서 필요로 하는 프리 필터를 목표 응답 전달함수로서 선택한 경우와 등가라고 여겨지고 있지만, 독립적인 아이디어에 의해 제안된 Data-Driven Closed-Loop Update Tuning(DD-CLUT)이라고 하는 방법도 흥미롭다. 그리고 FRIT 및 그것을 기초로 도출된 데이터 구동 예측과 동일한 개념을 주파수 영역으로 전개한 방법으로서 Virtual Time-response based Iterative Gain Evaluation and Redesign(V-Tiger)도 제안되어 있으며, 메카트로닉스계의 제진 문제 등 주파수 영역에서 생각해야 할 제어 사양에 관해서 위력을 발휘하는 방법으로서 기대된다.
그런데 취급되는 제어 문제의 확장이나 적용할 수 있는 제어 대상의 확장이라는 점에서도 유용한 성과가 나오고 있다. 우선, 제어 문제의 확장이라는 점에서 제어계 설계상 가장 먼저 생각해야 할 것은 안정성의 보증이다. 그러나 데이터 구동 제어에서는 안정성을 도모하는 근거인 수식 모델의 정보를 갖고 있지 않기 때문에 미해결의 문제이다. 단, 최근 안정 여유에 주목함으로써 안정성을 보증하는 데이터 구동 제어가 제안되고 있다.
또한 프로세스 제어계에서 중요하게 여기는 외란 인가 시에도 일정값으로 제어량을 유지하는 정치 제어 문제도 실용상 큰 의의를 가진다. 이 문제에 대해서는 일반화 최소 분산 제어에 근거한 방법이 제안되어 있다. 그리고 최근 보안 위험 대응에 관련된 연구도 이루어지고 있다.
데이터 구동 제어에서는 데이터 그 자체가 모르는 사이에 어떠한 변경을 당하면(독화), 생각한 것 같은 성능을 가지는 제어기를 얻을 수 없다. 이러한 독화를 검지하거나 견딜 수 있는 방법론이 필요한데, 그것을 생각하기 위한 공격 수단의 독화에 관한 연구도 보고되어 있다.
제어 대상의 확장이라는 점에서는 이론적 배경은 선형 시불변의 제어 대상이라는 것에 의존하고 있으며, 대상이 비선형인 경우에는 어떠한 방책을 취해야 한다. 여기서 비선형계나 시변계 등 다채로운 동특성에 따라 대응하기 위해서는 한 세트가 아니라 다수의, 더 말하면 데이터베이스 등에 격납되어 있는 대량의 데이터를 이용하는 것으로 대응하는 것도 메모리의 대량화나 계산기의 성능이 발전한 현재에는 하나의 유용한 활로라고 할 수 있다. 이러한 것을 배경으로 한 데이터베이스 구동형 접근법도 최근 활발하게 연구되어 본래의 목표 응답에 가까운 데이터를 몇 개 픽업해 그것의 온라인 학습에 근거한 제어기 파라미터의 튜닝 등이 제안되고 몇 가지 실용 예도 보고되어 있다.
마지막으로 모델 베이스드 제어와의 관계에 대해서 다루고자 한다. 데이터 구동 제어라고 해도 역시 수식 모델과는 떼어놓을 수 없다. 실제로 제어기의 갱신인 경우에는 사전 정보나 어떤 노미널한 모델을 기초로 설계한 제어기가 활용되고 있다. 또한 갱신법이 성능을 발휘한다고 하는 이론적 보증 뒤에는 수식 모델의 성질을 활용하고 있다. 이와 같이 모델 베이스드 제어와 데이터 구동 제어는 표리일체의 입장에서 각각이 보완되어 활용되어야 한다. 이 방면에 대한 최근의 흥미로운 연구로서 베이즈(Bayesian) 최적화를 이용해 근사 모델을 활용하면서 데이터로부터 제어 성능을 개선하는 방법이 제안되어 있다.
데이터를 직접 이용한 제어기 설계
그런데 앞에서 말한 갱신이나 조정을 메인으로 한 방향성의 연구와는 별도로, 그림 1의 B나 C와 같이 1990년 전후부터 데이터로부터 직접적으로 제어기를 설계하려는 연구도 이루어지고 있다. 이러한 흐름의 연구는 한동안 볼 수 없었지만, 2020년 전후부터 복각되어 매우 활발하게 연구되고 있는 분야이기도 하다.
우선 1990년대에 데이터와 수식 모델의 직접적 관계에 주목한 몇 가지 연구가 있었다. 구체적으로는 Ho-Kalman의 실현을 기초로 한 임펄스 응답과 최소 실현된 상태 공간의 {A, B, C} 행렬의 관계로부터 최적 레귤레이터의 상태 피드백 게인과 카르만 필터의 게인, 즉 LQG 제어기를 임펄스 응답 데이터로부터 구성하는 방법이 보고됐다.
또한 문헌 ‘Direct Construction of LQ Regulator Based on Orthogonalization of Signals’에서는 리카티(Riccati) 방정식의 해로부터 도출되는 이산 시간 최적 레귤레이터의 게인을 뉴턴법에 의해 순차적으로 푸는 알고리즘을 입출력 데이터로 기술함으로써 직접적으로 최적 게인을 구하는 방법을 제안하고, 출력 피드백의 경우로까지 확장하고 있다. 또한 데이터 구동 제어에서 취급하는 미지의 시스템에 대한 최적 제어의 접근법은 강화학습의 하나인 방책(제어 게인) 반복과도 대응하고 있으며, 제어와 강화학습을 관련시키는 영역으로서 최근에도 흥미로운 이론적 성과가 많이 나와 있다.
한편, 수식 모델과 해 궤도의 쌍대적인 관계에 주목한 연구도 보고되어 있다. 가장 쌍대적인 면을 강조한 방법은 문헌 ‘A Model-Less Algorithm for Tracking Control Based on Input-Output Data’에서 제안된 입출력 데이터 배열로 표현되는 데이터 공간에 기초한 모델리스 접근법일 것이다. 이것은 그림 1의 C에 해당하는 접근법이다. 예를 들면 1차 이산 시간계의 차분 방정식 표현은 y(t+1)+ay(t)=bu(t)로 나타내며, 수식 모델의 계수 {1, a, -b}를 세로로 배열한 열벡터는 이 시간 구간에서 관련된 데이터를 [y(t+1)y(t)u(t)]로 한 행벡터의 영화 공간에 속한다고도 볼 수 있다. 이것이 전체 시간 구간에서 성립한다고 생각하면, 이 행벡터를 적절한 수만큼 스택한 데이터 공간에서 동특성을 기술할 수 있다. 이 아이디어에 근거해 주어진 목표 궤도를 실현하기 위해 어떤 시각 t의 시점에서 얻은 적절한 크기의 데이터 공간 행렬로부터 다음의 t+1로 입력해야 하는 조작량을 계산함으로써 완전하게 수식 모델리스의 제어 방식을 실현한 것이 데이터 공간에 근거하는 모델리스 접근법이다.
다른 관점의 쌍대적인 접근법으로서 비헤이비어(behavior) 접근법에 기초하는 방법이 있다. 비헤이비어 접근법이란 시스템이 취할 수 있는 궤도(비헤이비어)에 주목함으로써 여러 가지 시스템 이론이나 시스템 설계를 종래보다 부감적으로 파악하려는 시도이며, 궤도 그 자체를 구성하는 변수도 입력과 출력을 구분하지 않고 외부 환경과 동특성의 정보를 주고받는 변수로서 파악하고 있다. 단, 대부분의 비헤이비어 접근법의 연구에서는 궤도를 직접 파악하는 것이 아니라 미분(또는 차분) 방정식의 집합에 의해 해 궤도 w를 R(σ)w(t)=0으로 나타내고 궤도를 제약하는 작용소 R(σ)에 초점을 둠으로써 시스템 해석을 하고 있다. 이러한 가운데서도 문헌 ‘Data-Driven Simulation and Control’에서는 작용소가 아닌 해 궤도 그 자체에 초점을 맞춤으로써 데이터 구동 제어나 시뮬레이션 방법을 제안하고 있다.
또한 2005년에 발표된 문헌 ‘A Note on Persistency of Excitation’에서는 앞에서 말한 작용소 R(σ)를 특정하기 위해 데이터 계열 {w(1), w(2), …w(N)}으로 구성된 한켈(Hankel)형의 블록 행렬에 대한 좌영화 인자가 R(σ)에 해당하는 것에 주목해 시스템의 수식 모델을 특정하기 위한 데이터 행렬의 조건은 무엇인가 하는 것을 이 데이터 행렬의 랭크 조건으로서 밝히고 있다. 이것이 앞에서도 나온 PE성이라고 하는 시스템 동정에서도 친숙한 동특성을 여진하기 위한 신호의 성질이라는 단어로 기술되고 있으며, 나중에 Willems의 fundamental lemma라고 불리는 보조정리가 된다.
그런데 그 후 2010년대의 종반 무렵, 이 Willems의 fundamental lemma를 기초로 한 Data-informativity라고 하는 개념 아래의 데이터 구동 제어를 위한 시스템 제어 이론이 제창된다. 예를 들면 {x(t), u(t)}, t=0, 1, 2, …, N이라는 입력과 상태의 유한 데이터를 얻었을 때, 각각

와 같이 데이터 행렬을 정의하면, 이에 적합한 수식 모델의 집합은  로서
로서

을 만족시키는 행렬의 세트 {A, B}의 집합이다. 여기서 데이터 D가 어떤 시스템론적 성질에 대해 Informative라는 것은 D에 적합한 임의의 {A, B}로부터 만들어지는 수식 모델로 표현되는 시스템이 그 성질의 조건을 만족시키는 것으로 되어 있을 때를 말한다.
이러한 관점으로부터 가제어성, 가관측성, 상태 공간의 상사 변환, 리아프노프 방정식, 상태 피드백, 옵서버, LQR, H∞ 제어, 소산성, 모델 예측 제어, 암호화 제어 등 모델 베이스드 제어에서 잘 알려진 시스템 해석이나 제어계 설계를 fundamental lemma 또는 Informativity의 관점으로부터 파악한 다양한 연구가 최근 3~4년 사이에 보고되고 있다. 수식 모델과 그 해 궤도로서 데이터 사이의 쌍대적인 관계를 감안해 일단 Informativity라는 개념으로 다시 파악할 수 있다면 이러한 많은 연구가 나타나는 것은 자연스러운 흐름이기도 할 것이며, 종래의 제어 이론에서도 그랬듯이 앞으로도 Informativity에 관한 다양한 연구 전개를 기대할 수 있다. 이에 관한 부감적 해설이나 각종 관련 문헌은 문헌 ‘Data-Driven Control’에 자세하게 나와 있다.
또한 Data-informativity에 근거한 이산 사상 시스템의 슈퍼바이저 제어도 발표되어 있으며, Informativity라는 개념이 다양한 시스템 이론을 포함하는 형태로 앞으로 부감적인 형태로 전개될 것으로도 기대된다.
맺음말
이상으로 관련 연구를 모두 다루었다고 할 수 있을지 모르겠지만, 데이터 구동 제어의 지금까지 흐름과 최근 연구 동향에 대해 간결하게 정리해 보았다.
데이터 구동 제어의 이론과 응용 양쪽의 관점에서 최신 연구 동향과 앞으로의 전망을 정리해 두는 것이 독자에게 의미 있다는 생각으로, 이후에 이어지는 관련 글에서는 최신 해설이나 사례 소개로 구성했다. 이 글이 데이터 구동 제어의 접근법에 익숙하지 않은 독자에게 살펴보고, 만져보고, 그리고 연구 방향성의 하나로서 또한 기술개발 활로의 하나로서 생각해 보는 계기가 되었으면 좋겠다.