구동 전류와 기계적 공진 사이 주파수 오프셋에서
로렌츠 힘 기반의 MEMS 지자기 센서 구동

공진 주파수 작동 시의 장점으로는 최대 감지 대역폭 증가, 단일 전류원을 통한 지자기 센서 작동 수 증가 가능성, 저전력 3축 자기장 센서 제조 등을 들 수 있다. 여기서는 구동 전류 주파수가 디바이스의 공진 주파수보다 다소 낮은 상태에서 로렌츠 힘 기반의 MEMS 지자기 센서를 작동시키는 부분에 대해 살펴보고, 로렌츠 힘 지자기 센서의 최적 설계를 위한 지침을 제공한다.

Giacomo Langfelder  Politecnico di Milano / Alessandro Tocchio  STMicroelectronics


현재 다양한 애플리케이션 분야[1], [2]에서는 3축 가속도 센서, 자이로스코프 및 3축 지자기 센서를 단일 칩에 통합하는 쪽으로 연구 초점을 맞추고 있다. 이와 같은 콤비 센서, 소위 9축 관성 측정 유닛(IMU : Inertial Measurement Unit)으로 GPS 신호 없이도 추측 항법 시스템을 통한 정밀한 동작 복원모션이 가능해진다.
최첨단 기술 분야에서는 MEMS 기술을 이용해 단일 칩에 구축한 6축 IMU[3], [4]의 예를 찾아 볼 수 있다. 현재로서는 스탠드얼론 디바이스나 9축 IMU에 탑재된 형태로 제공되는 이방성 자기저항(AMR)[5], [6] 기반 3축 지자기 센서, 혹은 자기 터널 접합(MTJ)[7]이나 홀 효과(Hall-effect)[8], [9] 기반 3축 지자기 센서가 관련 MEMS 제품보다 인기가 많다.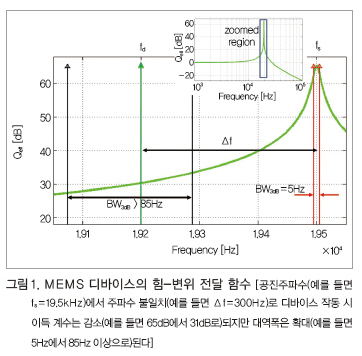


학계에서 MEMS 지자기 센서 몇 점을 선보인 적이 있었는데, 대부분 로렌츠 힘(Lorentz-force)의 원리(공진 시 주입된 전류로 모션 작동)를 기초로 하며 용량 리드아웃을 이용했다.[2], [10-13] 이러한 디바이스들의 성능은 대부분 단위 대역폭 및 단위 구동 전류 당 해상도(예: nT·mA/√Hz)로 비교할 수 있다.[14] 여기서는 선형 풀 스케일 레인지(FSR)뿐만 아니라, 전술한 다양한 기술 기반 디바이스를 비교하는 데 같은 파라미터를 성능 지수(FOM)로 사용한다.
지금까지 학계에서 연구하고 있는 공진 로렌츠 힘 디바이스의 문제점은 다음과 같다.
•‌이득 계수[여기서는 유닛 자속 밀도(Unit Magnetic Flux Density)당 정전 용량 변화로 정의]와 최대 감지 대역폭 사이에는 뚜렷한 상충 관계가 있는데, 이는 품질 계수에 대한 역 의존성을 나타낸다.
•‌평행판 용량 리드아웃 이용 시[1], 센싱 셀 수에 따라 이득 계수가 개선되지 않는다.
다음에 설명하는 ‘작동이론’에 있는 기타 문제점들은 공진 주파수에 안정적인 AC 전류를 정확히 주입하기 위한 오실레이터 구동 회로 실행과 관련되어 있다.
여기서는 주입된 로렌츠 전류의 구동 주파수 f_d와 기계적 공진 주파수 f_s 사이의 주파수 오프셋 Δf 상태에서 로렌츠 힘 지자기 센서를 구동하도록 제안한다(그림 1 참조). 이와 같은 접근법은 구동 및 감지 모드 간 주파수 불일치로 자이로스코프를 작동한 데에서 영감을 얻은 것이며,[15], [16] 다음과 같은 사항들이 고려된다.
•‌최대 감지 대역폭은 주파수 오프셋 Δf의 약 1/3까지 확장
•‌이득 계수는 공진 감지만큼은 아니지만, DC 이득의 30 배 이상
•‌구동은 약 f_d 수준에서 일어나며, 이는 높은 Q 계수 전달 함수 피크에서의 작동에 비해 상대적으로 플랫한 이득 계수 영역에 해당된다(그림 1 참조). 때문에 시스템은 제조 스프레드(Fabrication Spread)로 인한 주파수 오프셋 Δf의 소폭 변이 σΔf에 영향을 크게 받지 않는다.
•‌이와 같은 공정 변이(Process Variance)에 대한 낮은 민감도 덕분에, 주파수 fd의 단일 구동 전류로 3축 디바이스를 구동할 수 있으며, 이는 3배의 전력 소비 절약으로 이어진다.
다음에 설명하는 ‘작동 이론’에서는 공진 주파수와 제안된 주파수 분할에서의 로렌츠 힘 지자기 센서 가동 이론을 검토하고 비교한다. 그리고 ‘실험 결과’ 부분에서는 주파수 오프셋으로 구동했을 때, MEMS 지자기 센서의 이득 계수를 설명한다. 마지막으로, ‘추가 논의 및 결론’ 부분에서는 논의를 확대하여 로렌츠 힘 지자기 센서의 획득 가능한 FOM을 홀 효과 및 AMR 디바이스들과 비교한다.

작동 이론

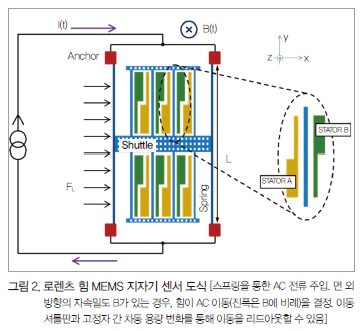
Z축 로렌츠 힘 지자기 센서는 그림 2와 같다. 지지 스프링은 한 쪽이 기판에 고정된 형태로 중앙 셔틀을 지지하는데, 이는 고정전극(고정자)과 함께 두 개의 차동 평행판 콘덴서 세트를 이룬다(각각 공칭 실험 값 C₀, 단면적 A의 N 셀로 형성, 플레이트 사이의 명목적 갭 g). 스프링을 통해 흐르는 AC 전류 i(t)는 z축 자축밀도의 컴포넌트 B가 있을 경우, 길이 L에 분산된 로렌츠 힘을 생성한다. 그 강도는 다음과 같다.



이 힘은 수평 방향으로의 이동 x를 결정한다. 이는 미분 커패시턴스(Differential Capacitance) 변화인 ΔC로(작은 변위 근사로) 해석할 수 있다[ε0를 진공 유전율(Permittivity of Vacuum)로 가정].[17]

1. 공진 주파수 작동
첫번째 모드의 기계적 공진 주파수 fs에서 디바이스가 작동할 경우(x 방향 이동에 상응), 힘-변위 전달 함수는 DC 강성도 k에 관해 품질 계수 Q 로 증폭된다. 따라서, 식 (3)과 같이 된다.

분모의 2는 스프링으로 분산된 힘에 해당한다. 작동이 분자류 영역에서 발생한다면(0.1∼10mbar 압력 범위로 패키지된 MEMS의 경우 다수 발생), 이득 계수는 참고문헌 [2]와 같다.

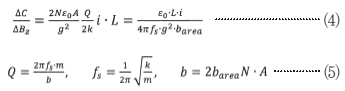
상기 공식에서 b는 감쇠계수(Damping Coefficient)이다. 이 파라미터는 평행판의 페이싱 길이에 선형 의존적인 것으로 알려져 있다.[18] 매달린 무게 높이를 고정 공정 변수로 가정하면, b는 단위 영역당 값 barea로 나타낼 수 있다. m은 유효 디바이스 무게(Effective Device Mass)가 된다. 공진 가동의 경우, 고유의(디바이스에만 해당) 신호 대 잡음비는 열기계적 잡음 SF,n에서 시작되는 변위로 나타낼 수 있다(N2/Hz 단위).

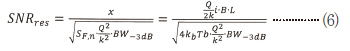
－3dB 리드아웃 대역폭 BW_-3dB은 품질 계수로 결정된 값과 같다고 가정할 수 있다(BW_-3dB＝f_s/2Q). SNR＝1로 설정함으로써 감지 가능한 최소 자속밀도 변이를 도출할 수 있다.

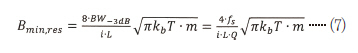
넓은 대역폭은 낮은 품질 계수 및 해상도의 악화를 뜻한다. 영역(길이), 전력 손실(전류), 대역폭이 애플리케이션 사양으로 고정되면 민감도를 개선하기 어려운데, 민감도[식 (4)]는 센싱 셀 수 N의 영향을 받지 않는다.
공진 주파수에서 스프링을 통해 전류를 주입하는 데 필요한 회로에 대해서는 다음과 같이 설명할 수 있다.
•‌루프에 지자기 센서의 기계적 공진기(Resonator)를 포함하지 않은 오실레이터 회로(개방 루프)는 불가능한데, 이는 공진 주파수와 품질 계수가 공정 변이, 온도 및 노후화의 영향을 받기 때문이다. 자이로스코프의 경우[15], 이러한 요인들은 허용할 수 없는 이득 계수의 변화를 초래한다. 다양한 환경 조건에 따라 부분별, 혹은 각각의 디바이스에서 이와 같은 변화가 발생할 수 있다.
•‌또한 공진 주파수에서 폐쇄 루프 오실레이터(즉, 공진 요소로 디바이스를 탑재한 오실레이터[19])를 통해 구동 회로를 구현하는 것도 어렵다. 이는 정전류 및 오실레이터의 루프 이득이 센싱 방향의 자속밀도 강도 B의 영향을 받기 때문이다.
•‌세 개의 다른 센싱 구조를 가진 3축 실행의 경우, 공칭 주파수 f_s에서 같은 전류원으로 구동하기 어렵다. 이는 공정 변이로 인해 세 MEMS가 동일하게 설계돼도, 보통 서로 다른 피크 주파수를 보여주기 때문이다(z축 디바이스를 위한 것이지만 x축 또는 y축도 마찬가지다[13]).

2. 주파수 분할 구동
이득 계수를 감소시키고 대역폭을 확장하는 방법은 지자기 센서의 공진 주파수 f_s와 구동 전류 주파수 f_d 사이에서 분할로 구동하는 것이다. 이 상황에서 개방 루프 구동 전류 fd는 전자 오실레이터 또는 보조 MEMS 공진기 기반 오실레이터에서 얻을 수 있다. 부분 간 주파수 분할 Δf에서 변이 σΔf와 온도에 따른 변화가 크게 감소하므로 후자의 경우가 더 선호된다. 이는 공진기와 지자기 센서 설계 시 그 주파수를 공정 및 온도 변화에 의해 유사한 영향을 받도록 할 수 있기 때문이다.[15] 일반적인 경우, 로렌츠 힘과 지자기 센서 이동 간 라플라스 전달 함수는 식 (8)과 같다.

로렌츠 힘 주파수 fd에 대한 계수(오프셋 Δf＝f_s－f_d로 적절히 주입된 전류로 실행)는 s＝jωd, ωd＝2πfd와 ωs＝2πfs 세팅으로 도출할 수 있다.

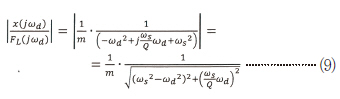
Q >>1이고 주파수 분할 Δf가 fs보다 크게 낮은 경우, 전달 함수는 다음과 같이 단순화된다.

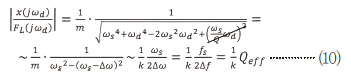
여기서 Qeff는 유효 품질계수(Effective Quality Factor), 즉 공진 주파수 fs에서의 오프셋 Δf로 얻은 잔류 증폭(Residual Amplification)을 말한다. 그러므로 신호 대 잡음비는 다음과 같다.

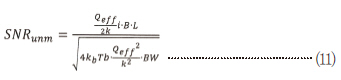
여기서 BW는 그림 1에 나타난 ±3dB 값 내 폭의 전자식 필터를 뜻한다(fd에서의 디모듈레이션 후 적용된 것으로 생각할 수 있다). 최소 감지 신호는 BW와 감쇠계수(Damping Coefficient)의 영향을 받는다.

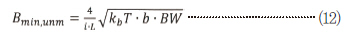
식 (6)과 식 (11)을 비교하면 유사한 점을 발견할 수 있다. 같은 대역폭에 대해 비교하면(BW＝BW-3db), 최대 SNR을 가진 시스템이 단순히 b에 대한 최저값을 가진 것으로 나타난다. 이에 따라 감쇠계수 b가 낮아질수록 SNR이 개선된다는 것을 알 수 있는데, 이것은 그리 놀라운 사실이 아니다. 중요한 것은 주파수 불일치 시, b를 줄이면서(기하학적 구조나 압력에 의해 움직임) 대역폭 BW에 영향을 주지 않을 수 있다는 (전자부품에 따라 결정) 것이다. 반면에, 주파수 일치 시 BW-3db에 영향을 주지 않고 b를 변경할 수는 없다.
다른 시각으로 보면, 불일치 작동 시 대역폭은 주파수 오프셋과 관련된 분수 부분까지 확장될 수 있다. 이 때 b가 적절히 감소된다면 고유 SNR을 좋게 유지할 수 있다. 공진 최대값을 전자 필터링할 때에는 주의가 필요하다.[15]
수치적인 예를 살펴보면, 20kHz 주파수에서 공진하는 품질계수 1800의 디바이스는 대역폭이 5Hz일 것이다. 오프셋 300Hz의 같은 디바이스는 약 100Hz의 ±3dB 대역폭(주파수 일치 시보다 높은 자릿수)에 도달할 수 있다.
SNR 및 최소 감지 자속밀도는 디바이스 노이즈만 가리킨다. 전자 노이즈에 대한 내용은 ‘추가 논의 및 결론’ 부분에서 소개한다. 결국 주파수 오프셋이 클수록 공정 변이에 대한 내성이 커진다. 그 결과, 다음과 같이 된다.
•‌구동 오실레이터의 실행 문제를 잠재적으로 해결할 수 있다(오실레이터 주파수가 의도된 fd와 정확히 일치하지 않으면 문제되지 않는다).
•‌동일한 공칭 공진 주파수 fs를 가진 3축 디바이스는 실제 주파수(명목상 동일하지만)가 Δf보다 상당히 낮은 양만큼 차이가 있다고 나타날 경우(예를 들면 공정 변이 또는 수치 시뮬레이션 편차 때문) fd에서 단일 전류로 구동될 수 있다.

실험 결과

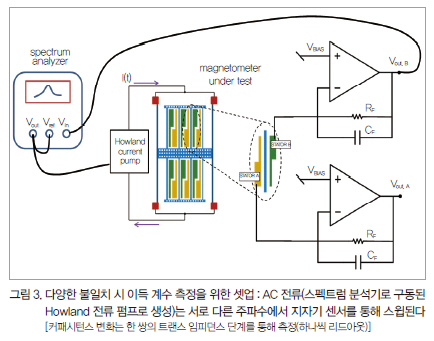
구동 전류와 공진 최대값 간 주파수 오프셋으로 디바이스의 이득 계수를 테스트하기 위해 그림 3과 같이 설정했다. 로렌츠 힘 지자기 센서는 스펙트럼 분석기를 통해 주파수가 스윕된 전류를 통해 작동된다. 미분 커패시턴스 변화는 MΩ의 피드백 저항을 가진 한 쌍의 디스크리트 부품 트랜스 임피던스 앰프(TIA)를 통해 측정할 수 있다. 영구 자석(상대적 거리는 sub-mm 정밀도로 변경 가능)을 통해 생성된 세 가지 다른 자속밀도로 반복 측정된다. 다른 필드의 방해를 피하기 위해 상대적으로 낮은 구동 전류 최대 진폭(|i(t)|∼300
μArms)에서 상대적으로 높은 자속밀도(B > 1mT)로 측정된다. B의 셋업 조정은 사전에 아사히 카세이(Asahi Kasei) 레퍼런스 홀 타입 지자기 센서를 통해 이루어졌다.[20]
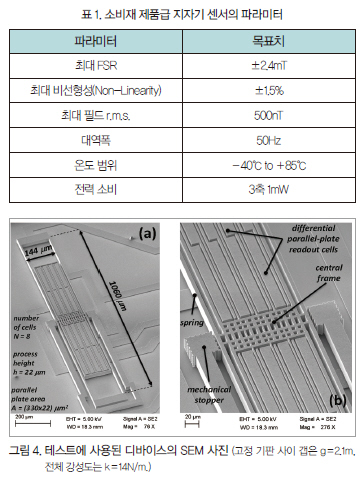
테스트에 사용된 MEMS 지자기 센서는 ST마이크로일렉트로닉스의 ThELMA(Thick Epitaxial Layer for Microactuators and Accelerometers) 공정으로 생산됐다.
이 디바이스의 주사전자현미경(SEM : Scanning Elec- tron Microscope) 사진과 관련 디멘션은 그림 4에서 확인할 수 있다. 공칭 공진 주파수는 설계상 약 20kHz로 설정되어 있는데, 이는 공진 주파수로 작동되는 다른 가전제품에서 주로 발생하는 음파 방해를 피하기 위해서이다.[21]
측정 결과를 그림 5에 나타낸다. x축은 구동 전류 주파수 f_d, y축은 두 TIA의 차동 출력(Differential Output)이다. 공진 최대값은 고정자에 전압 V_BIAS＝1V로 18.94kHz에서 발생한다(TIA의 가상 접지를 통해 적용). 최대 민감도(공진 시)는 약 0.3mV/mT(품질 계수 약 360)로, (4)의 이론상 예측 값과 맞아 떨어진다. 이에 상응하는 대역폭은 BW_-3dB＝26Hz라는 것을 쉽게 알 수 있다. 그러므로 이득 계수와 대역폭의 곱은 7.8Hz mV/mT이다. 그림은 공진 최대값 f_s와 관련해 주파수 오프셋 Δf(200-600Hz)에서의 반응을 나타낸 것이다.
그림 6(a)는 그림 5를 심화한 것으로, 자속밀도 B의 함수로 출력전압을 보여주며 서로 다른 Δf의 매개 곡선도 나타낸다. ΔC/ΔB·Δf 곱의 항등성(Constancy)은 그림 6(b)에서 알 수 있는데, 여기서 점선 곡선은 7.8Hz mV/mT에서의 이론적 함수를 나타내며 점들은 실험 포인트이다.
노이즈 성능은 현재 셋업에서 TIA 단계의 피드백 저항 R의 존슨 소음(Johnson Noise)으로 제한된다. 이는 스펙트럼 분석기의 리드아웃 대역폭 BWSA∼30Hz(BW_-3dB과 유사하게 설정)에서 통합된다.

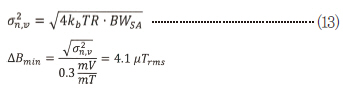
이에 따라 고유의 최소 측정 필드는 검증할 수 없었다. 다음에는 리드아웃 전자제품에 요구되는 노이즈 성능을 살펴본다.

추가 논의 및 결론

지금까지의 분석 및 결과를 소비재 애플리케이션(네비게이션, 헤딩, 전자 컴퍼스 등)에 적용해 본다. 시행 기술(AMR, MTJ, 홀 효과 등)에 관계 없이 향후 일반적으로 요구되는 조건을 표 1과 같이 요약할 수 있다.
비교를 위해, 다른 최신 디바이스의 파라미터 및 단위 소비전류당 해상도로 정의된 성능지수(FOM)를, 상응하는 FSR과 함께 표 2에 나타낸다.

1. 최소 필드 및 상응하는  
커패시턴스의 변화
약 1°의 헤딩 정밀도를 보장하기 위한 최소 감지 자속밀도는 약 500nT이다.[10] ‘작동 이론’ 부분에 나타난 디바이스를 사용하면, 저소음 전자제품으로 공진 작동 시 최소 측정 가능 자속밀도를 최대 주파수 BW-3db∼26Hz(Q＝360, 1mbar)에 따라 식 (7)과 같이 구할 수 있다.

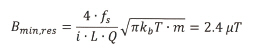
해상도나 대역폭 모두 표 1의 사양에 들어가지 않는다. 품질 계수를 개선하기 위한 압력 감소는 대역폭에 부정적인 영향을 미칠 것이다. 3축 디바이스의 경우, 전류 i의 3배가 필요하다는 것을 고려했을 때, 이 작동 모드의 FOM은 약 420μT·μA/√Hz이다.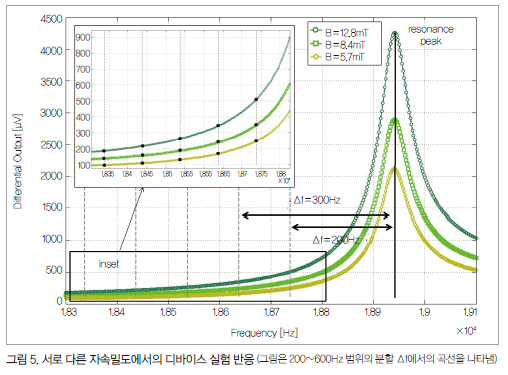


한편, 같은 기기를 주파수 분할 300Hz, 전자 필터링 대역폭(예, 복조 후 적용) 50Hz, 게터 물질을 사용하는 산업 공정으로 얻을 수 있는 최저 압력 ∼0.05mbar(Q∼7200), 식 (12)의 최소 측정 가능 자속밀도를 적용하면 다음과 같이 된다.

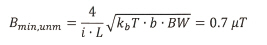
공진 작동 대비 3.5배 개선되고, 표 1의 요건에 근접하며 상응하는 FOM은 대략 ∼29μT·μA/√Hz이다.

2. 추가 개선 사항
앞에 나온 파라미터를 사용하면, 최소 감지 커패시턴스는 다음과 같이 된다.

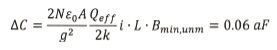
리드아웃 전자기기의 요건 완화를 위해 학계에서도 상대적으로 낮은 전류[22, 23]로 sub-zF/√Hz 해상도를 측정해 왔지만, 최소 필드에 따라 커패시턴스 변화를 개선하면 좋을 것이다.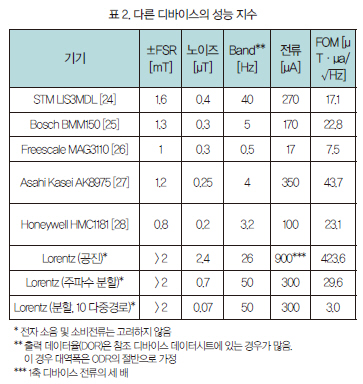


이미 알려진 기술로는 다중 경로를 이용해 디바이스에서 동일 전류를 몇 차례 재순환하는 것이 있다.[11] 초소형 기계물질에 절연된 금속 스트립을 용착해 경로를 형성한다. Np 다중경로 접근법은 출력 신호가 동일 배수로 클 것이라는 점을 암시한다. FOM은 Np배 낮고 동일 자속밀도에 대한 커패시턴스 변화는 Np배 크다. 예를 들어, 참조 논문과 같이 Np＝10인 경우 이전 상황의 동일 자속밀도에 대해 다음과 같은 결과를 얻게 된다.

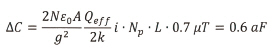
이와 같은 커패시턴스의 변화는 상대적으로 저소음, 저전력인 전자부품으로 리드아웃할 수 있어[24] 전자부품의 소음을 우선적으로 배제할 수 있다. 이와 유사하게 전자 소비 전류는 디바이스에서 소모되는 것에 비해 극히 소량으로 간주될 수 있다.

3. 선형성 및 FSR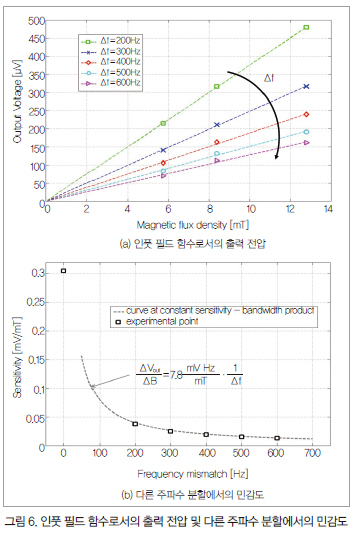


로렌츠 힘의 원리가 선형(Linear)이므로, FSR의 경우 평행판 리드아웃에서 제한이 있을 수 있다. 그러나 참고문헌 [14]와 같이 적은 변위 및 차동 구성으로 인해 획득 가능한 선형 FSR은 작동 원리에 내재적인 비선형성을 가진 다른 기술(예를 들면, AMR 기기)보다 상당히 크다.
결국 FSR은 ADC에서 사용한 비트수 Nbit에 따라 제한될 것이다.

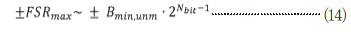
표 2를 통해 오랫동안 과학계의 관심을 받아온 로렌츠 힘 디바이스가 주파수 분할로 작동했을 때 첨단 미래 제품 대비 경쟁력이 높을 수 있고, 다중경로 설계가 기술상 가능할 경우 첨단 디바이스를 뛰어넘을 수 있다는 것을 알 수 있다.
앞으로도 주파수 분할 작동에 최적화된 3축 지자기 센서 설계 및 그에 상응하는 저소음, 저전력 구동을 위한 통합 회로 설계에 힘써야 할 것이다.