카오스 제어 103회
기계공학에서의 비선형 특성

이번 호는 기계공학 비선형 특성으로서 비고전적인 집중 시스템에서의 충격 발진을 중심으로 카오스 현상과 비선형 현상에 대한 지금까지 연구된 문헌을 설명한다.

소개

전통적인 설계 도구들과 조절기들은 영점 틈새 해석(zero-clearance analysis)에 기반을 두며, 접촉 손실에 대해서 설명하는 것은 부적절하다. 진동-충격 동력학들의 최근 개발들은 틈새, 백래시(backlash)와 자유 플레이(free-play) 비선형성을 가진 기계 시스템과 전자 기계 시스템의 설계 도구를 수정하는 우수한 기초를 구성한다.
이와 같은 시스템들의 사례는 자유 트러스트 구조에서 기계적 접합, 우주 제어 표면에서 자유 플레이, 회전 기계에서 마찰-충격과 마이크로 액추에이터에서의 충격을 포함한다. 이들 시스템 동적 특성의 최근 개발들을 설명한다. 가장 중요한 응용은 인간 발성 주름 충동이며 이것은 조직 손상에 영향을 준다. 발성 주름의 몇몇 비선형 2차원 모델들에 대해서도 설명한다.

기계적 접합

기계적 접합들은 다른 형태 속에서 존재하며 기계 기구의 설계와 구성, 다체 시스템, 우주 트러스트 구조, 항공기 날개-축적 커플링 시스템에서 필수적이다. 접합 갭들에서의 충격은 낮은 주파수 전역 모드(global mode)에서 낮은 주파수 지역 모드(local mode)까지 진동 에너지 전달의 원인이 될 수 있다.
기계적 접합에서의 접촉 손실은 접촉이 다시 구성될 때 시스템에서 충격을 줄여주는 원인을 제공할 수 있다. 정상적으로 핀으로 고정한 접합들은 핀들과 U자형 고리들/돌출 끝 부속품 사이 틈새의 작은 양을 가진다. 작은 갭들은 트러스 구조의 제동과 동력학에서 특별히 접합이 데드 밴드(dead-band) 영역을 횡단할 수 있을 때 매우 중요한 변화의 원인이 될 수 있다. 접합들에서 매우 작은 갭들은 일반적으로 카오스 동력학을 유도할 수 있는 비선형성을 생성한다. 우주 구조들에서 카오스 동력학들은 과도 발진을 감쇠시키기 위한 능동 제어 시스템의 설계에서 몇몇 어려움을 부과한다.
Moon과 Li는 고정 접합된 우주 트러스트 구조의 동력학을 연구했다. 이 실험 결과들은 정현파 여기 하에서 광대역 카오스와 유사한 진동을 보여주었다. 압축 부하가 있는 구조에 장력 케이블이 추가될 때 카오스 레벨은 감소된다. 탄성 접합에서 동적 접촉들은 비선형 스프링과 제동기로 구성하는 비선형 접합 모델에 의해 시뮬레이션 됐다.
Dubowsky와 Freudenstein은 틈새를 가진 탄성 기계적 접합의 해석적 모델을 공식화했고 이는 기계적 시스템과 전자기계적 시스템을 다룬다. 이들은 동적 힘 증폭, 주파수 응답, 시간-변위 특성과 다른 동적 특성들을 추정했다. 이것은 탄성 충격-쌍 모델이 동적 특성의 다양성을 나타낸다는 것을 보여주고 있다. Heiman 등은 기저 질량을 가진 경사진 슬롯에서 이동하는 데 제한을 가진 2차 질량과 발진 기저로 구성되는 경사진 충격 쌍의 동력학을 고려했다.
변경 충격에 대한 2차 질량의 동력학들은 기저 운동의 1주기에 대하여 맵의 항에서 공식화되었다. 정상 상태 2:1 운동, 이들의 안정도와 이어지는 주기 배증 분기들이 추정되었다. 질량이 없는 링크 모델과 같은 유용한 해석적 도구들은 복잡하고 계산적으로 비싸다.
Earles과 Seneviratne는 질량이 없는 링크 모델을 이용한 접속 손실의 현상을 연구했다. 질량이 없는 링크는 기본적으로 잉여 자유도로서 접합 제거를 모델링한다. 이들은 접합 제거를 가진 4개-바 기구의 운동 방정식을 유도했다. 그런 후 이 방정식들은 시스템 운동 변수와 제거 링크 응답의 항에서 접합력 진폭 제거를 위한 표현을 만들기 위하여 분리한다. 이것은 제거 접합에서 접촉 손실 조건을 조절하는 단일 영-제거 무차원 파라미터가 존재하고 있음을 보여주고 있다.
Pereira와 Nikravesh은 간헐성 운동으로 진행하는 기계적 시스템의 해석을 위한 계산적 기구를 제시했다. 운동 방정식의 표준형은 좌표의 최소 집합을 가지고 유도되었다. 이들 방정식은 물체 운동량, 속도 불연속과 리바운드에서 점프를 계산하는 충격 주기에 걸쳐 시스템의 운동량 평형을 위한 절차를 사용했다. 이 작업들은 제한된 운동량에서 점프가 식별되는 개루프와 폐루프 기계 시스템에 확장되었다.
Folkman 등은 핀으로 고정한 접합을 가진 3개의 격실 트러스트의 제동 특성을 측정했다. 시험 결과들은 고정 핀을 가진 접합들이 중력에 의존하는 제동을 가질 수 있음을 이용한 구조임을 검증했다. 제동률들은 중력 유도 부하들의 변화로 인하여 5까지 상승하는 인자에 의해 변화됨을 알았다. 이 변화는 1-g 환경에서 우주 구조를 특성화할 때 매우 중요할 수 있다. 충격 결과의 결합 갭으로서 개방과 폐쇄가 저주파 전역 모드로부터 고주파 지역 모드까지 진동 에너지가 전달됨을 찾았다.
Berzi 등은 결합 슬리브 접합의 비선형 스프링 질량 모델에 대한 식별 접근법을 개발한 것이다. 강성, 마찰, 질량 파라미터들은 접합의 시뮬레이션과 측정된 응답들 사이의 차이의 최소화에 의해 결정된다. 이것은 재료 제동을 통하여 에너지 소산의 비율에서 증가와 관련된다.
Flores 등은 다체 시스템의 운동학과 동력학 위의 공간 접합의 접합 제거 영향을 연구했다. 해석적 접근법은 기본적인 요소들이 베어링 받침인 회전 접합을 위해 개발됐다. 특정의 작업조건 아래서 이 2개의 기계적 요소들은 각각 충돌한다. 연속적인 접촉력 모델은 접촉 충격력을 평가하기 위해서 채택되었다.

우주선 구조에서의 자유-플레이

우주선 구조에서 자유-플레이 비선형성 효과들은 몇 개의 연구 주제가 되었다. 예를 들어 Laurenson와 Trn은 자유-플레이 비선형성의 제어 표면을 가진 미사일의 동요를 조사했다. 특별한 비행 속도에서 외부 여기에 의해 원인이 된 발진 진폭이 구축된다는 사실을 알았다. 발진의 진폭 증가를 가진 조합에서 자유-플레이 비선형성의 존재로 인하여 시스템의 유효 강성은 증가했고 이 운동은 몇몇 제한된 진폭에서 안정하게 된다.
Kim과 Lee는 제한 사이클 발진을 포함하는 응답과 카오스 운동이 자유-플레이 비선형성을 가진 에어포일에서 피치 대 플런지(pitch-to-plunge) 주파수 비율에 따라 높게 영향받았음을 찾았다. 피치에서 자유-플레이 비선형성을 가진 날개 모델의 실험적 연구들은 이중 리미트 사이클 발진의 출현을 보여주었다.
Alighanbari는 보조 날개 힌지 모멘트에서 자유-플레이 비선형성을 가진 3자유로 에어포일-보조 날개 동력학을 연구했다. 분기 해석은 선형 다양한 펄럭거리는 경계 아래에서의 우물에 대한 다양한 리미트 사이클 발진을 나타내었다. 초기 조건에 의존하고 공기 속도, 준주기, 카오스 발진 등이 보조 날개 운동에 대하여 보고했다.
논문의 연속선상에서 Bae와 Lee, Bae 등은 리미트 사이클 발진의 다양한 형태와 주기 운동 상의 자유 플레이와 쌍선형에 의해 표현된 구조적 비선형성의 영향을 고려했다.
Zentner와 Poirion은 정규적인 기판 구조로부터 분리된 접촉을 해야만 하는 자유도에서 모드 합성에 기반한 차수 모델 저감 방법을 개발했다. 이 공식은 접촉 문제의 비평활 동력학에 대한 Moreau’s 이론의 직접 응용을 허용한다. 이들 접근은 제어 표면 연결에서 자유-플레이를 가진 항공기 날개에 의해 주어진 것으로서 유체-구조 결합 시스템에 적용된다.
제어 표면 자유-플레이를 가진 일반적인 날개부의 비선형 돌발 답 해석은 Tang 등에 의해 제시되었다. 피치 자유에서 구조적 자유 플레이 형태 비선형성을 가진 2-자유도 날개부는 Marsden과 Price에 의해 아음속 풍동에서 실험적으로 시험됐다. 공기 탄성 응답 상의 자유-플레이 효과가 연구되었고 플러터(flutter) 속도는 자유-플레이 길이가 증가함을 가지고 감소됨이 찾아졌다.
자유-플레이가 존재하는 것과 존재하지 않는 날개-저장을 가진 실험 모델들이 플러터와 리미트 사이클 발진에 대하여 Tang과 Dowell에 의해 설계되었다. 이 날개는 일정한 두께의 단순 평판으로서 모델링되었다.
이 스토어는 2개의 지지점을 통하여 날개를 가지고 결합된 가느다란 강체로서 모델링되었다. 앞에 있는 지지점은 날개에 접합되었으며 뒤에 있는 지지점은 자유-캡을 가진 스프링을 통하여 날개에 연결되었다. 이 설계는 피치에서 오직 운동을 가지는 스토어를 허용한다. 이러한 배열에서 스토어 비선형성은 주로 자유-플레이 때문이다. Tang과 Dowell은 날개 응답 진폭 상의 날개-저장 모델에서 자유-플레이의 효과를 실험적으로 해석적으로 시험했다. 이것은 날개의 돌발 응답 진폭은 자유-플레이 갭 또는 돌발 각도 증가로서 증가한다는 사실을 알았으며 이는 거의 스토어 피치의 초기 조건에 거의 독립적이다.

회전자의 마찰-충격 동력학

동작하는 회전 기계에서 회전부와 고정부 사이의 엄청난 마찰은 회전자의 유해한 불안정성을 유도할 수 있다. 마찰을 하는 동안 마찰과 관련된 충격, 강성과 결합 효과들과 같은 동력학 현상이 발생할 수 있다. 회전자/고정자 시스템 사이에서 이따금 부분적인 마찰은 강한 비선형 시스템을 형성한다.
베어링 틈새를 포함한 비선형 회전자 시스템들은 문헌적으로 광범위하게 연구되었다. 이 연구들은 섭동 기법, 고속 푸리에 변환 절차를 가진 고조파 평형 기법을 함께 이용하여 슈퍼하모닉과 서브하모닉 응답을 추정하는 데 초점을 맞추었다.
회전 기계에서 마찰-관련 현상에 대한 초기 작업의 평가는 Muszynska에 의해 제시되었다. 이러한 심각한 문제는 모든 항공기 엔진 고장의 약 10%에 달하는 것으로 조사되었다. 마찰과 충격의 주요 원인은 회전자와 케이싱 사이의 작은 틈새의 존재로 인함이며 회전자와 회전자 원심력의 대량 불평형 존재 때문이다.
회전자와 케이싱 사이 접촉상의 건식 마찰은 다른 인자를 구성한다. Muszynska 등은 우주 왕복 주요 엔진 고압 연료 터보-펌프를 시뮬레이션하는 회전 기계에서 회전자-대-정지 요소 마찰의 문제를 시험하기 위한 해석적 실험적 조사를 수행했다. 이들은 마찰 조건하에서 회전자/베어링/봉입 시스템의 해석적 모델을 개발하고 수치적으로 동적 회전자 응답을 추정했다. 추정된 결과들은 실험적 측정과 잘 일치하고 있음을 알 수 있었다.
Goldman과 Muszynska는 틈새와 충격을 가진 회전 기기의 시뮬레이터로부터 몇몇 실험적 결과를 제시했다. 분기도들은 수치적으로 생성되었으며 안정함을 나타내고 카오스 응답 경계를 보여준다. 그들은 외부 주기 여기 하에서 충격과 틈새를 가진 구조에서 주요와 고차 공진의 존재를 구성했다. 비접촉에서 접촉 상태로의 천이들이 변수 강성, 제동, 충격과 간헐성 마찰에서의 결과로 나타냄을 찾았다.
회전자와 고정자 접촉에 대하여 Goldman과 Muszynska는 시스템의 전역 거동을 가진 국부 방사와 접선 효과를 상관하는 모델을 개발했다. 이 모델에 기반한 회전자/고장자 시스템의 수치 시뮬레이션의 결과들은 분기도의 형태, 회전자 측면 진동 시간 기반 파형과 궤도로 제시되었다. 이 시스템은 강성 비대칭으로 인하여 진동의 추가적인 서브하모닉 영역을 나타내는 것이 관측되었다. 이후에 Goldman과 Muszynska는 회전이 없는 성분을 가지고 주기 접촉을 경험하는 회전자의 측면 진동을 고려했다. 비탄성 충격의 경우, 이 시스템은 구분 스텝-변화 강성으로 기술했다. 또한, 특수한 좌표 변환이 평활 연속 힘에서 불연속성을 변환하기 위해 소개되었다. 이 변환은 회전자 측면 운동의 불평형 관련 공진 영역의 변화를 시험하기 위하여 평균 기법과 같은 전통적인 기법을 이들에게 적용했다.
Wei 등은 회전 기계의 고정자와 회전자 사이의 마찰 상호작용의 주요 특징을 강조했다. 회전자/고정자 마찰에 의해 유도된 접촉력들은 시스템 강성이 증가하는 것에서 찾아졌다. 시스템 충격의 발생은 심각한 과도와 비선형 특성들이 생성되었다. 더욱이 접촉에서 회전자와 고정자 사이의 상대 운동으로 인한 마찰력은 회전자의 역회전 운동과 정상 응력 조건들에 대하여 심각한 영향을 주는 마찰의 원인이 될 수 있으며 회전자의 국소 열적 왜곡을 생성할 수 있다. 더욱이 이 접촉은 시스템에서 뒤로 충격력을 공급하는 결합 효과를 소개했으며 이는 더욱더 회전 기계의 동작 조건을 복잡하게 한다. 이들은 충격력의 피드백을 수행함에 의해 회전자-고정자 마찰의 해석적 모델을 제안했다.
다른 속도 값에서 마찰의 응답 특성들이 간단한 회전자/고정자 시스템에 기반하여 시험됐다. 몇몇의 실험 결과들은 여기에서 수치적으로 예측된 것과 비교했다. 카오스 운동은 Piccoli과 Weber에 의해 마찰 회전자 시스템에서 실험적으로 관측되었다. Chu와 Zhang은 회전 속도가 증가함으로써 마찰-충격의 발생 이후에 카오스에 이르는 3개의 경로를 식별했다. 이들은 주기 배증, 그레이징 분기와 주기 운동에서 카오스로의 갑작스러운 천이이다. 준주기 운동들 또한 보고되었다.
전력용 MEMS(microelectromechanical systems)에서 마이크로-회전자 기계에 대한 마찰-충격을 가진 Jeffcott 회전자 시스템의 일반 모델 마찰 해의 안정도가 Zhang과 Meng, Zhang 등에 의해 연구되었다. 회전 속도, 불평형, 제동 계수와 마이크로-회전자 시스템 응답의 마찰 계수의 효과들이 시험되었다. 이것은 시스템 파라미터가 변화됨으로써 주기, 준주기, 카오스 운동 중에서 마찰 변경 크기 효과를 가진 마이크로-회전자 시스템에서 마찰 효과를 보여주고 있다.
Popprath와 Ecker는 비선형 접촉력을 통하여 회전자 모델을 가지고 상호작용하는 고정자를 가진 Jeffcott 회전자 모델의 간헐성 접촉을 시험했다.
Banakh와 Nikiforov는 링과 케이싱 사이의 건식 마찰뿐만 아니라 링과 회전자 사시의 틈새에서 유압력이 있을 때 회전자와 유동 봉입 링 사이의 진동-충격 상호작용을 연구했다.
Han 등은 주기, 준주기, 복잡 운동들에서 결과인 고정된 제한기(limiter)를 가진 회전자 시스템의 마찰-충격을 보여주었다.
Azeez와 Vakakis는 시계열 데이터로부터 지배 간섭성 구조를 추출하는 적당한 직교 분해의 기법을 이용하여 회전자 동적 시스템의 진동-충격 동력학을 연구했다. 강체 제한을 가진 회전자 시스템에 대한 단일 마찰-충격 주기-n 운동의 존재에 대한 조건은 Li와 Lu 등에 의해 해석적으로 유도되었다. 스케일로그램과 웨이브렛 위상 스펙트럼이 Peng 등에 의한 마찰-충격을 가진 회전자-고정자 시스템의 동적 거동을 특성화하기 위해 소개되었다. 회전자와 고정자 사이의 마찰-충격으로 인한 음향 방사는 마찰 위치에서 탄성 변형의 원인이 된다.
이와 같은 음향 방사는 Yongyong에 의해 마찰-충격 고장을 진단하고 식별하기 위해 사용됐다. 이들은 실험적으로 회전자-베어링 시스템에서 마찰-충격의 음향 방사 특성들을 분석했다. 음향 방사와 진동 신호들이 마찰-충격 식별을 위한 음향 방사 기반 기법의 우수성을 검증하기 위하여 비교되고 해석됐다. 웨이브렛 스케일로그램이 마찰-충격 음향 방사의 주파수 분산 특성과 전파 특성, 시간 주파수 특징을 분석하기 위하여 사용됐다. 이 결과들은 마찰-충격 음향 방사가 다중-모달 탄성파에 기인한다는 것을 나타내고 이는 주로 휨파(flexural wave)와 확장파(extensional wave)를 포함한다.

사례연구

Li와 Pa ı doussis은 2-자유도 시스템에 의해 모델링된 회전자-케이싱 시스템에서 마찰-충격-문제를 연구했다. 회전자의 병진 속도에서 갑작스러운 변화는 복원 계수 e와 건식 마찰 계수 μ를 소개함에 의해 모델링되었다. 그림 1의 기준을 가지고 정상(방사 e_r과 접선 횡방향 e_θ) 성분의 항에서 각각의 속도 벡터로 식 (1)과 같이 분해될 수 있다.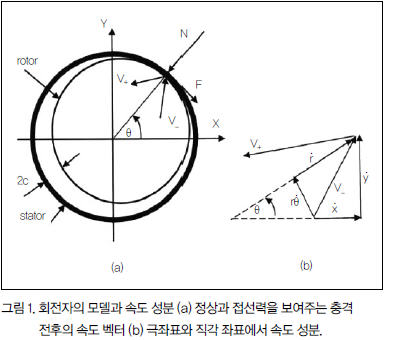



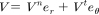(1)

충격 이전의 정상 속도 V_{_}ⁿ 과 충격 이후의 정상 속도 V₊ⁿ 에서의 충격은 충격 법칙에 의해 식 (2)와 같이 표시한다.

(2)

충격 이후의 접선 속도는 차단 계수 B의 항으로 식 (3)과 같이 정상 방향과 접선 방향 모두에서 회전자의 선형 충격의 원리 적용에 의해 주어진다.

(3a)

(3b)

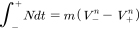
쿨롱 마찰력 F=μN(여기서 F, N은 충격 순간에서 회전자의 마찰력과 정상력)의 정의를 소개하는 것은 식 (4)와 같이 충격 후의 접선 속도를 세울 수 있다.

(4)

여기서 B=μ(1+e)V_{_}ⁿ/V_{_}^t 는 브레이크 계수이다.
만약 B≥1이면 충격에 대한 V_{_}^t 가 존재한다. B의 표현은 이것이 양의 값과 음의 값을 가질 수 있다는 것을 보여준다. 충격이 발생하는 것에 대하여 V_{_}ⁿ은 양의 값이 되어야 하고 따라서 V_{_}^t 는 정방향 회전일 때 양의 값이거나 역방향 회전일 때 음의 값일 수 있다. 만약 V_{_}^t >0이면 회전 운동의 선행 방향은 회전자의 방향과 동일하다. 한편 만약 V_{_}^t <0이면 회전자 중심 운동은 시계 방향으로 가속되며 에너지는 외부 구동 토크로부터 온다.
회전자 질량 불평형과 영의 초기조건의 영향 아래서 Li와 Pa ı doussis은 원심 파라미터와 e=0.9의 복원 계수 고정값에 대한 건식 마찰 계수 항에서 회전자의 다른 정상 상태 운동의 영역을 얻었다. 그림 2는 그림 3개의 영역을 보여준다.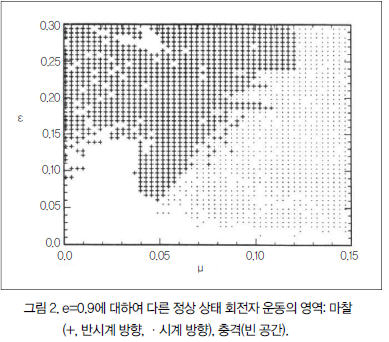



첫 번째 영역은 고정자에 대하여 회전자의 시계방향 마찰을 나타내는 점에 의해 점유된다. 이 운동은 ‘dry whip’이라 불리거나 후방 마찰로 불린다. 두 번째 영역은 교차에 의해 점유되며 각 교차는 회전자 운동과 동일 방향(반시계방향) 또는 전향 마찰에서 파라미터 쌍의 결과를 나타낸다. 빈 공간 영역들은 충격 운동을 나타낸다. 그림 3은 e=0.075에 대하여 마찰 계수 u의 각 값에 대한 사전-충격 정상 상태 방사속도 기록에 의해 구축한 분기도를 보여준다.



μ≤0.019에 대하여 오직 유한적인 충격 속도의 많은 값이 존재하며 이는 해들이 주기적이거나 준주기적임을 나타낸다. μ=0.02의 이웃에서 회전자 운동은 카오스이다. 마찰계수에서 더욱 증가시키면 마찰 계수 범위 0.0212≤μ≤0.0242에서 다시 주기 운동으로 돌아온다. 위에서 방사 속도의 범위는 다중 값을 가정하는 것으로 시작한다. μ≥0.02875에 대하여 분기의 다른 집합이 발생하며 이는 카오스 운동을 이끈다.
Qin 등은 회전자와 베어링을 가진 회전자와 고정자 사이의 접촉을 연구했다. 이것은 마찰이 그레이징 분기를 생성함이 찾아졌다. 회전 속도, 불평형과 외부 제동과 같은 시스템 파라미터의 변화를 가지고 주기 배증 분기와 토러스 분기와 같은 복합 응답 특성이 관측됐다. 질량-불평형을 가진 마찰-충격 회전자 베어링 시스템의 일반 해석적 모델이 Shen에 의해 개발됐다. 이 모델은 방사 탄성 충격과 접선 쿨롱 마찰로 구성된다. 질량 원심력의 존재에서 분기도는 제어 파라미터로서 회전을 취함에 의해 생성된다. 이것은 회전자의 질량 원심력이 마찰-충격 회전자 베어링 시스템의 운동 특성상에 필수적인 효과를 본다는 것을 알았다.
Yue·Gang 등은 회전자 베어링 마찰-충격 동력학의 연구에서 비선형 마찰력과 비선형 기름막 힘의 영향을 고려했다. 이것은 상대 속도의 계수 증가를 가진 준주기 운동과 카오스 운동 영역 모두를 증가하는 준-임계 속도 범위 내에 있음을 보여주고 있다. 초임계 속도 범위 내에서 카오스 운동 영역은 감소하고 있음이 찾아졌다. 그러나 마찰 충격력은 증가하고 준주기 운동들은 점진적으로 3주기가 된다. 이들 특징은 마찰 충격 고장에서 회전자-베어링 시스템의 고장 진단을 위한 이론적 기초로써 사용되었다.
터보 기계의 고정자 구조와 회전자 블레이드 사이의 마찰은 Sinha, Chu과 Lu에 의해 시험되었다. 일정한 각속도를 가진 회전하는 Timoshenko 빔 스피닝의 반복된 팁 충격의 비선형 동적효과는 Sinha에 의해 연구되었다. 진동-충격 시스템들의 미분 방정식에서 파라미터의 불연속으로 인하여 과도 응답은 복잡한 동적 거동을 나타낸다. Jeffcott 회전자의 6자유도에 대응하는 축 마찰-충격 모델은 Yuan에 의해 개발되었다. 질량 불평형과 축 마찰-충격 효과들이 고려되었다. 이것은 축-마찰 충격의 동적 거동은 방사 충격으로부터 완전히 구별되며 축 진동은 축 마찰-충격의 진단에 필수적이라는 결론을 내리게 된다.

마이크로 액추에이터

몇몇 마이크로 액추에이터들은 대규모 변위를 생성하는 반복된 충격을 수행하도록 설계되었다. 예를 들어 평활 충격 선형 모터는 우수한 액추에이터 중의 하나이다. 이것이 간단한 구성임에도 불구하고 선형 액추에이터는 동작의 2개 모드로 인하여 긴 스트로크와 높은 위치 분해능을 검증한다. 하나의 모드는 긴 스트로크 구동이며 다른 모드는 위치 구동에 관한 것이다.
Yamagata와 Higuchi는 압전 액추에이터에 의해 생성된 충격력에 의해 구동된 운동 기구로 구성한 위치 시스템으로 구성한다. 이 시스템은 건식 마찰과 충격성 관성력을 이용한다. 마이크로 또는 나노 로봇에서 2자유 또는 그 이상의 자유도에서 고정밀 운동은 주요 요구 사항의 하나이다.
Zesch 등은 2개의 압전 소자를 개발하는 스위스 ETHZ 나노 로봇 프로젝트에 대한 몇몇 기본적인 구동 기구를 설명했다. “Abalone”은 충격 구동 원리에 의존하는 3자유도 시스템이다. 6um 미세 위치의 액추에이터의 국소 범위 내의 범위 조정과 10nm 이상의 분해능이 가능하다.
‘NanoCrab’은 스틱-슬립(stick·slip) 효과에 의존하는 베어링이 없는 회전 마이크로 모터이다. 종단 적재 압전 캔틸레버의 충격력에 의해 액추에이트된 병진과 회전 운동에 대한 2자유도를 가진 정밀한 액추에이터는 Zhang에 의해 제시되었다. 회전운동과 병진운동 상의 액추에이터 성능이 측정되고 큰 여행거리, 강한 구동 능력과 고속 위치 분해능을 나타내게 되 었다.
Mita 등은 정밀하고 무제한 변위를 만들 수 있는 마이크로머신 액추에이터를 개발했다. 이 충격 액추에이터들은 그림 4에서 보여주는 것과 같이 프레임, 현수, 구동 전극, 스토퍼(stoppers)에 의해 지지되는 이동 가능 질량으로 구성되어 있다. 이동 가능한 질량의 충격은 동작의 근원이다.



이동 가능한 질량은 질량과 전극 사이의 정전기력에 의해 가속된다. 이것은 액추에이터의 기저에 고정된 스토퍼와 충돌한다. 충격력이 최대 정전 마찰을 넘어설 때 액추에이터는 이동하기 시작한다. 이 액추에이터는 마찰력의 저항으로 인하여 궁극적으로 멈춘다. 현수된 마이크로 질량은 2개의 유리 평판 사이에 봉입되어 있고 정전력으로 구동된다.
Zhao와 Dankowicz 등은 Mita 등에 의해 최초로 개발한 충격 마이크로-액추에이터의 거의 그레이징에 가까운 동력학을 해석했다.
마이크로 액추에이터의 충격과 비충격의 분기 거동은 주기당 비충격의 하나와 충격의 하나를 가지고 주기 충격 궤도의 항에서 논의되었다. Kang 등은 이산 시간 이벤트에 의해 인터럽트된 마이크로 액추에이터의 분기 해석을 위한 계산 툴박스를 개발했다. 다중 세그먼트 주기 해 궤적들의 가지들이 단일 파라미터 변화아래서 지속되었다. 이것은 또한 주기 배증의 궤적, 안장점 노드에 대응하는 분기 곡선을 제공했으며 그레이징 분기점들은 2개 파라미터 변화아래서 계속되었다.
Zhang 등은 MEMS 스위치와 테이핑 모드 AFM과 같은 마이크로 발진기의 충격 동력학을 이해하기 위한 구분 비선형 모델을 제안했다. 변형이 비선형 주파수 응답 영역에서 발생한 테이핑에서 고려했다. 연화(softening) 효과와 경화 (hardening) 효과 모두가 고려되었다. 비선형성은 분기 지역으로 이동할 뿐만 아니라 테이핑 이벤트 대역폭의 변화가 있음이 찾아졌다. 실험과 수치 사이의 결과 비교가 고려된 구분 비선형 모델의 유용성을 검증했다. 보상-느슨함 하이브리드 기계 시스템 분류의 피드백 제어는 비제어 부분과 제어 부분으로 구성하며 이는 Brogliato와 Zavala-Rio에 의해 연구된 충격 법칙과 일방적인 제한에 의해 연결되었다. 이 접근은 Zavala-Rio와 Brogliato에 의해 제시된 1자유도의 저글러(juggler) 제어의 중요한 확장에 기반한다. 이의 안정화 특성의 시스템의 다양한 물리적과 제어 특징 특성을 고려했다. 이후에 Menini와 Tornambe은 액추에이터된 선형 기계적 시스템하에서 비평활 충격이 중심이 된 저글러의 특별한 등급을 고려했다. 이것은 전체적인 시스템이 제어 가능하고 단지, 충격은 데드-비트(dead-beat) 조절 문제를 풀기 위해 사용될 수 있다는 것을 보여준다.
Sokolov 등은 동기 형태의 액추에이터를 이용하여 전자와 전기-기계적 피드백을 가진 자기-유지 발진 시스템으로서 공진 발진 장비를 설계하기 위한 자동 공진 여기로 알려진 새로운 접근법을 소개했다.
동기 액추에이터들은 주파수가 부하에 의존하지 않지만, 전력 공급의 주파수에 오직 의존하는 여기력을 생산한다. 이것은 자동 공진 접근이 진동과 진동-충격 기계에 대한 전자기적 액추에이터에서의 원래부터 가지고 있는 결점을 극복할 수 있음을 검증했다. 자동 공진 시스템의 기본적인 아이디어를 그림 5에 보여준다.
그린 5(a)는 센서와 증폭기로부터 제한 출력을 가지고 진동 신호의 위상을 이동한 피드백 설계 기구를 보여준다. 이 액추에이터는 신호를 여기력으로 변환한다. 진동의 결과인 피드백 회로에서 주어진 위상 이동을 가지는 것은 피드백이 없는 기계적 서브시스템의 자연 주파수로서 동일한 주파수를 가지는 것이다. 그림 5(b)는 구형 펄스 힘이 여기에 사용된 반면 속도 신호는 피드백에서 사용한 것에 대한 매트랩 시뮬링크 모델이다. 구형 펄스 여기와 속도 모두의 시계열 기록은 그림 5(c)에 보여주고 있다. 물리적 위상 이동은 진동의 공진 모드를 제공하기 위해 요구되지 않는다. 나중에 Babitsky와 Sokolov, Voronina 등은 기계 응용에 대하여 초음파 트랜스듀서와 요소적 전자기 액추에이터를 가진 간단한 진동-충격 시스템에서 자동 공진 제어를 고려했다. 이것은 자동 공진 접근이 진동 기계에서 전자기 액추에이터의 응용을 개선한다는 것을 나타낸다.



진동 충격 하에서의 진동 보호

충격 부하와 충격과 관련된 시스템들은 심각한 진동을 나타내고 이들은 특별한 격리 방법이 필요하다. 충격 적재는 유압 해머, 선박과 바다 구조상의 물의 파동 동작에서 강타하는 부하, 강체 또는 탄성 정지를 가진 진동 시스템들과 같은 많은 기계적 응용과 만나게 된다. 이들 원하지 않는 외란에 대하여 주어진 물체를 보호하기 위하여 진동 보호 시스템은 진동원과 물체 사이에 놓일 수 있다.
이들 연구에서 Alabuzhev 등은 0에 가까운 강성을 가진 진동 보호 시스템을 소개했다. 그림 6은 부하 베어링 탄성 요소가 음의 강성을 가진 소자뿐만 아니라 일정한 양의 강성을 가진 선택된 시스템의 개략도를 보여준다.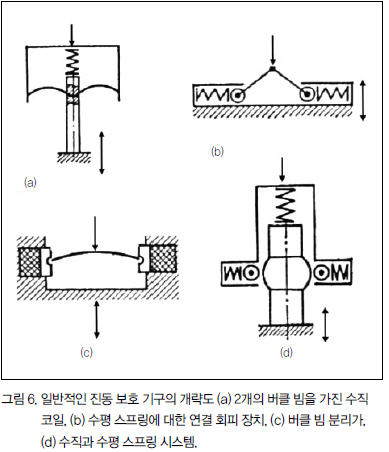



분리기의 이 형태는 차량에서 운전자 의자들의 진동 격리, 소형 기계의 충격 활동, 철도차량 현수 장치에 대하여 사용해왔다. 음의 강성을 가진 시스템은 Gerner 등과 Yashin 등에 의해 연구되었으며 카오스 운동 영역에서 이와 같은 시스템의 성능은 Lee, Goverdovskiy 등에 의해 시험되었다.
능동 제어 방법이 없는 비선형 분리기의 최근 개발의 포괄적인 평가는 Ibrahim에 의해 제시되었다. 충격 부하에서 중심이 된 강체 구조를 수행하는 격리 실장의 비선형 특성의 몇몇 수정은 Dufour에 의해 제시되었다. 이 수정은 잘 설계된 거동 달성을 위하여 진동 충격에 대응하도록 채택되었다. 소형 도구로부터 생성한 진동에 대한 작업자의 보호는 특별한 진동 방법을 요구한다.
Dobry와 Brzezinski은 도구와 손잡이 사이의 상호작용을 최소화하기 위한 강한 탄성 비선형 격리기를 개발했다. 충격 충격성 부하로부터 부상을 방지하기 위한 노력으로 Balandin 등은 충격 격리 시스템의 제한 성능 해석을 다루는 연구 활동의 개요를 제시했다.
Shu와 Shen, Zhiqing와 Pilkey은 웨이브렛 변환을 통한 기계적 시스템의 최적 충격과 충격 격리를 연구하기 위한 제한 성능을 수행했다. 김발 전자-광학 소자의 범퍼를 가진 진동 보호 배열은 Veprik에 의해 개발되었다. 이 소자는 적외선 초점 배열의 냉각을 위한 분리 스터링 크라이 냉각기(split Sterling cry cooler)에 기반하여 설계되었다. 확대된 진행을 가진 범퍼의 설치는 사고 충격의 확률을 줄여주고 초과되는 편향을 효과적으로 줄여준다. 그러나 범퍼의 존재는 진동 격리 배열이 반대의 특성을 가진 잠재적인 강한 비선형 진동-충격 시스템 속으로 돌아온다.
이들 특성을 제거하는 효과적인 방법에서 Babitsky와 Veprik는 최소 자유 여행 거리를 가지고 설치된 최적으로 제동된 범퍼의 조합에서 비제동되고 저주파 진동 분리기를 사용하는 협력에 기반한 새로운 개념을 소개했다. 몇몇 분리기는 구분 선형 또는 비선형 함수로서 표현될 수 있는 이들 파라미터의 값에서 갑자기 변화하는 경험을 한다. 이것은 유연한 분리기들이 분리를 위해 가장 좋은 것으로 알려져 있다. 그러나 비선형 경화는 높은 진폭에서 상대적 변위를 최소화하는 것이 요구된다.
Patrick와 Jazar는 높은 상대 변위의 제한에서 2차 현수를 소개했다. Mahinfala는 포화 스프링 요소를 가진 진동의 주파수 응답 연구를 위해 쌍곡선-접선 포화 함수를 채택했다.
Deshpande 등은 구분 선형 표현에 의해 기술된 높은 비선형 시스템 연구를 위해 채택된 평균 접근법을 채택했다. 이들은 정상 상태하에서 쌍선현의 주파수 응답에 대한 명시적 함수를 얻었다. 이 함수는 점프 회피에 대하여 시험했으며 조건은 점프의 원하지 않는 현상이 발생하지 않는다는 것을 보장하기 위해 유도되었으며 이 시스템 응답은 기능적이고 유일하다.
Orzechowski는 비선형 실장의 거동을 연구했으며 임펄스 입력에 대한 그들의 응답을 측정했다. 그들의 결과들은 시스템에서 추가 제동 없이 충격으로 인하여 이 응답의 과도 몫을 줄이는 선형성 실장의 제한을 보여주고 있다. 장벽의 존재는 공진 이웃에서 특별히 상대적 진폭을 넘어서는 것으로부터 진동 시스템을 방지하는 것으로 알려져 있다.
분리기에서 종단 정지의 효과는 Narimani, Golnaraghi 등에 의해 연구되었다. 이들은 시스템의 상대 변위를 최소화하는 구분 선형 시스템을 채택했고 파라미터의 범위를 식별하기 위하여 평균법을 적용했다. 이것은 제동비가 구분 선형 진동 분리기에서 강성보다 더 지배적임을 알았다.

배영철 전남대학교 공과대학 전기공학과 교수(ycbae@chonnam.ac.kr)