1차 측 제어(Primary-Side-Regulated, PSR) 플라이백 컨버터는 LED 드라이브 시장과 여행용 어댑터의 휴대 전자 시장에서 널리 사용되는 일반적인 컨버터이다. 1차 측 제어는 컨버터의 1차 측으로부터 파형을 관찰하여 플라이백의 출력 전류 또는 출력 전압을 조절하는 것으로 이루어진다. 따라서 이 기술은 옵토커플러, TL431 또는 출력 전압을 감지하는 연산 증폭기를 제거하여 전원 공급 장치의 부품자재를 줄이는 데 도움이 된다. 게다가 PSR은 출력 전류를 감지하는데 필요한 센싱 저항 회로부를 절약할 수 있다. 일반적으로 PSR에서 출력 전압 정보는 보조 권선을 통해 획득될 수 있다는 것이 잘 알려져 있다. 또한 출력 전류는 1차 측 모스펫(MOSFET) 전류 감지를 통해 추정될 수 있다. 그러나 이 기법으로 제어 매개변수에 대해 어느 정도의 정밀도를 기대할 수 있는가?

LED 드라이버 제조업체들은 일반적으로 주어진 입력 전압에서 +/- 5 %를 목표로 삼는다. 본 논문은 최악 조건 회로 해석(Worst-Case Circuit Analysis, WCCA) 기법들을 사용하여 플라이백 출력 전류의 정확도 추정과 +/- 5 % 목표에 대한 획득 결과의 직접적인 대비 방법을 자세히 설명한다. 본 논문의 첫 번째 부분에서는 PSR의 분석 모델을 소개하고 있다. 또한 이 첫 번째 부분은 출력 전류에 대한 몬테카를로 분석(Monte Carlo Analysis)에 초점을 맞출 것이다.

PSR 플라이백

참고 문헌 [1]은 플라이백 컨버터의 2차 측 제어(Secondary-Side-Regulated, SSR)와 1차 측 제어(Primary-Side-Regulated, PSR)  버전의 차이점을 설명하고 있다. 

그림 1은 2차 측 정전류 (Constant Current, CC) 및 정전압 (Constant Voltage. CV) 제어를 사용하는 SSR 플라이백 컨버터의 회로도를 보여 준다. 2차 측 부품자재(BOM)는 매우 중요하다.  (연관된 보상 회로망이 있는) 한 연산 트랜스컨덕턴스 증폭기 (Operational Transconductance Amplifier, OTA)는 출력 전압을 감지하는 반면 다른 하나는 출력 전류를 감지한다. Sink 전류가 큰 OTA는 또 다른 OTA를 배제하며, 옵토커플러를 통해  설정치를 지정하게 된다. 출력 전류 값에 따라 OTA 전력 손실이 전원 공급 장치의 효율을 떨어뜨릴 수 있어서 저항기는 출력 전류 감지에 필요하다. 반면 PSR 플라이백은 그림2에 제시된 것처럼2 차 측 부품자재를 감소시킨다.

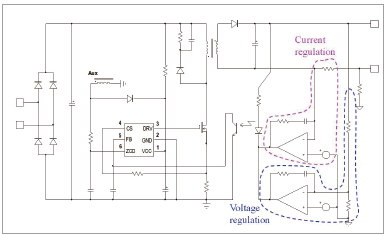
▲ 그림 1. 간략화된 2 차 측 정전압 및 정전류 제어 플라이백 컨버터

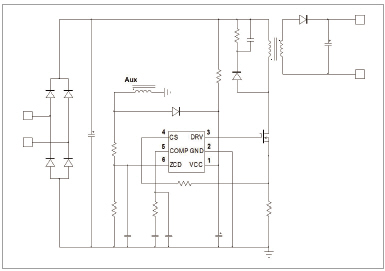
▲ 그림 2. 간략화된 PSR 플라이백 회로도

PSR 정전류/정전압(CC/CV) 컨버터는 일반적으로 경계선 전류 모드 (Borderline Conduction Mode, BCM) 또는 불연속 전류 모드 (Discontinuous Conduction Mode, DCM)로 작동한다. 출력 전압은 보조 권선 전압 감지에 의해 제어된다. 실제로 보조 권선은 전력 모스펫(Power MOSFET)의 비작동 시간 동안 출력 전압의 정보를 제공한다. 컨트롤러는 (core demagnetization를 나타내는) 보조 전압 변곡점(Auxiliary Voltage Knee)을 샘플링함으로써 출력 전압을 정확하게 제어할 수 있다. 정전류 제어의 경우는 1 차 측에 출력 전류의 직접적인 이미지가 없다는 점에서 정전압 방식과 차이가 있다. 출력 전류은 다음 단락에서 볼 수 있듯이 코어 감자 시간과 전원 스위치 내부 전류 측정을 통해 추정된다.

출력 전류 분석 수식

출력 전류 정확도를 측정하기 위해서는 PSR 정전류 - 전류 플라이백 모델이 필요하다. 그림 3은 BCM에서 작동하는 플라이백 컨버터의 1차 및 2차 측 전류를 보여준다. MOSFET이 켜지면 컨트롤러 IL,pk 에 의해 지정된 설정치에 도달할 때까지로  “입력 전압 Vin / 1차 인덕턴스 Lp” 와 거의 동일한 기울기로 전류가 상승한다. MOSFET이 꺼지면 누설 인덕턴스 전류는 자화 전류에서 빠지며, 출력 전류 증가를 지연시킨다. 그 결과 2 차 피크 전류가 감소된다.

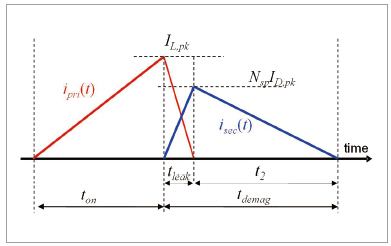
▲ 그림 3. BCM에서 작동하는 플라이백 컨버터의 1 차 및 2 차 전류 파형

여기서

-ID,pk는 2 차 정류기 피크 전류를 나타낸다.

-Nsp는 플라이백 트랜스포머의 권수비를 나타내며, 1차 권선 횟수에 의해 나눠진 2차 권선 횟수와 동일하다. (Nsp = Ns/Np)

출력 전류는 한 스위칭 주기 Tsw 동안의 평균 파형 isec(t) 또는 단순히 그림1의 파란색 삼각형 영역을 나타낸다. 출력 전류 수식은 (1)로 표현된다.

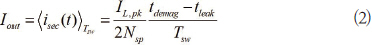
여기서

- tdemag는 변압기의 감자 시간(demagnetization time)을 나타낸다.

- tleak는 누설 인덕턴스를 재설정하는 데 필요한 시간을 나타낸다.

출력 전류에 대한 이 식을 살펴보면 권수비 Nsp 는 상수라는 것을 알 수 있다. 이것이 전류 모드의 정전류 제어가 일반적으로 수행하는 것이다. 대부분 경우 사람들은 출력 전류에 대한 누설 인덕턴스 효과를 간과하고 단순히 출력 전류를 제어하기 위해 감자 시간(demagnetization time)만을 모니터링하는 경향이 있다.

결국, PSR 컨트롤러는 다음과 같이 피크 전류를 제어하는 알고리즘을 구현한다.

또는

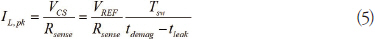
여기서

-VCS는 컨트롤러에 의해 표시된 전류 감지 전압을 나타낸다.

-Rsense는 MOSFET전류를 감지하는 저항기를 나타낸다.

-VREF는 컨트롤러가 내부적으로 제공하는 정확한 기준 전압을 나타낸다.

-Tsw는 스위칭 주기를 나타낸다.

수식 (3)에서 수식 (4)로 정의된 피크 전류를 대입하면 출력 전류에 대한 최종식이 도출된다.

처음에 수식 (6)을 보게 되면, 출력은 자화 인덕턴스와 무관한 것처럼 보인다. 또한 Nsp는 변압기 권수비를 나타내기 때문에 Iout 정밀도는 오직 VREF와 Rsense 정밀도에 의해서만 좌우된다.

실제로 컨트롤러 및 전원 스위치 드라이브에 내재된 내부지연 (tprop)으로 인해 피크 전류는 Lp 및 Vin 에 따라 약간 증가하게 된다. 수식 (4)는 다음과 같이 업데이트된다:

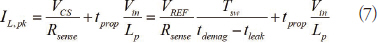
PSR 컨트롤러는 지연에 의해 발생하는 피크 전류 증가를 보완하기 위해 입력 전압 함수를 고려하여 피크 전류 설정치를 감소시키는 수단을 특별히 제공하고 있다. 이를 일반적으로 라인 피드포워드 (line feedforward )라고 일컫는다. 간단한 해결책은 라인 전압에 비례하는 전류 감지 전압에 오프셋을 추가하여 구성하는 것이다. 따라서 Vin 이 증가함에 따라 피크 전류가 감소하게 된다. 예를 들어, 그림 4는 NCL30082 PSR 컨트롤러 내부에 구현된 라인 피드포워드 회로를 보여 준다.

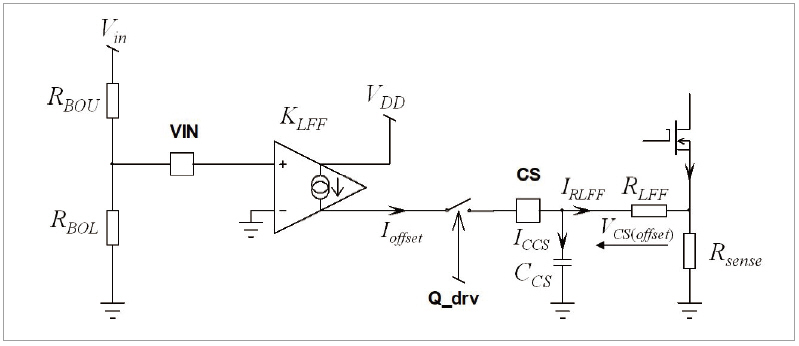
▲ 그림 4. NCL30082 내부에 구현된 라인 피드포워드 회로

여기서

-VCS(offset)는 PSR 컨트롤러의 라인 피드포워드 회로에서 생성되는 오프셋 전압을 나타낸다.

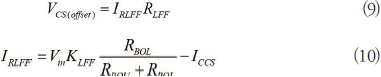
IRLFF는 RLFF 내부에 흐르는 전류를 나타내고, ICCS는 작동 시간 동안 오프셋 전류 Ioffset 가 CS 핀에 인가될 때의 CS 핀 커패시터 충전 전류를 나타낸다. 라인 피드포워드 회로는 본 논문의 2부에서 상세 설명될 것이다.

피크 전류 설정치는 컨트롤러에 의한 트랜스포머 감자 시간(Demagnetization Time) tdemag 의 정확한 측정에 의해 결정된다. 이 감자 시간은 비작동 시간 동안 보조 권선 전압(Auxiliary Winding Voltage) Vaux 의 변곡점을 감지하여 측정된다 (그림 5). 보조 권선은 컨트롤러의 ZCD 핀으로 모니터링 된다 (그림 1). R-C 회로망은 드레인-소스 전압(Drain-Source Voltage) 이 최소값일 때 MOSFET을 작동시키기 위해 보조 권선 전압 Vaux 를 약간 지연시키는 ZCD 핀에 연결된다. 이 드레인-소스 최소 전압을 대개 곡전압(Valley)이라고 하다. R-C 회로망은 변곡점(Knee) 감지를 지연시켜 컨트롤러에 의해 측정되는 감자 시간 tdemag 을 인위적으로 증가시킨다. 

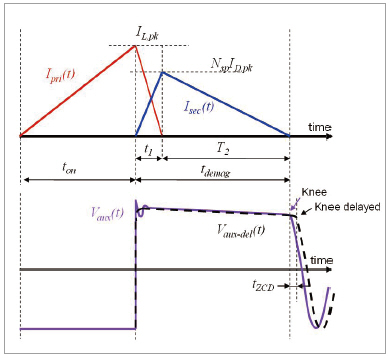
▲ 그림 5. 보조 권선 파형

이 회로망의 시간 상수값이 높으면 출력 전류에 큰 영향을 줄 수 있다. 따라서, 이 사항은 분석 모델에서 고려될 필요가 있다. tZCD 를 R-C 회로망에 도입된 지연(Delay)이라고 한다면 수식 (8)에 나타난 피크 전류를 다음과 같이 업데이트할 수 있다.

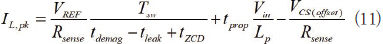
첫 번째 근사치로, 지연 tZCD 은 ZCD 핀 R-C 회로망의 시간 상수(Time Constant )와 같다고 간주할 수 있다.

여기서

-RZCD 는 컨트롤러의 ZCD 핀에서 볼 수 있는 등가 저항을 나타낸다. 

-CZCD 는 컨트롤러의 CZD 핀과 GND 핀 사이에 연결된 커패시터 값을 나타낸다.

올바르게 설계된 1차 측 제어 정전류 플라이백(PSR CC Flyback)을 위해서는 tZCD 는 20ns ~ 300ns 범위의 값이어야 한다.

컨버터의 분석 모델을 구축하기 위해서는 수식 (11)에서 누설 인덕턴스 리셋 시간 tleak에 대한 수식을 찾을 필요가 있다. 참고 문헌 [2]는 변압기의 누설 인덕턴스에 따른 RCD 클램프회로부 설계에 대한 상세 설명을 제공하고 있다.

그림 6을 살펴보면 RCD 클램프는 MOSFET이 꺼지는 경우 누설 인덕턴스 Lleak로 인한 드레인 전압 상승을 제한한다. 누설 인덕턴스에서는 RCD 클램프(Vclamp)의 클램프 전압에서 플라이백 컨버터의 반사 전압(reflected voltage)을 뺀 것과 동일한 리셋 전압 Vreset 이 나타난다. 따라서 누설 인덕턴스 전류는 기울기 SLleak 로 감소한다.

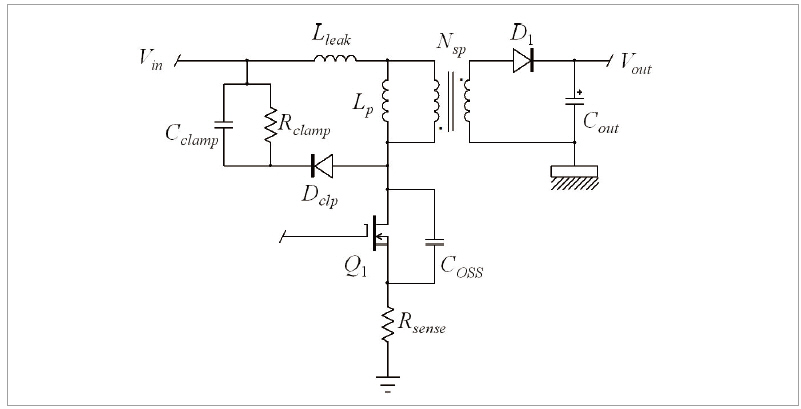
▲ 그림 6. 플라이백 컨버터 및 클램프 회로망

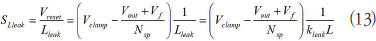
수식 (13) 에서 Lleak 은 계수 kleak 로 표현되는 1 차 인덕턴스의 백분율로 나타낸다.

다음과 같은 tleak 식을 추론할 수 있다.

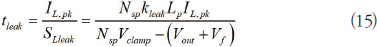
참고 문헌 [2]에 따르면 유사 공진 컨버터(Quasi-resonant Converter)에 대한 tdemag 와 Tsw 의 수학적 표현식은 다음 수식을 통해 근사치 계산을 할 수 있다.

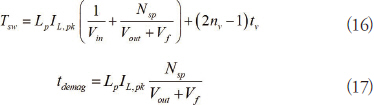
여기서

-nv는 동작하는 Valley전압 번호(Operating Valley Number)를 나타낸다. 첫 번째 Valley 전압 작동시 nv = 1, 두 번째 Valley전압 작동시 nv = 2

-tv는 자유 진동 반주기(Free Oscillation Half Period )를 나타낸다.

수식 (18)에서 Clump 는 드레인 노드에서의 총 커패시턴스를 상징한다. 이는 MOSFET 드레인-소스 커패시터 및 권선들과 1차 인덕턴스 간에 분리된 다양한 변압기 커패시터를 포함한다.

-Vf는 2 차 정류기 순전압 강하(Secondary Rectifier Forward Voltage Drop)를 나타낸다.

수식 (11) 에서 수식 (15), (16) 및 (17) 을 결합하면 피크 전류는 다음과 같이 업데이트될 수 있다.

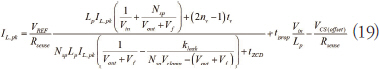
수식 (19)를 살펴보면, 컨버터가 제공하는 피크 전류 설정치는 1 차 인덕턴스(Primary Inductance), 지연(Propagation Delay) 및 클램프 전압(Clamping Voltage)에 의해 좌우되는 것을 알 수 있다. 따라서 이들 매개 변수들은 또한 수식 (6)이 나타내는 것과 반대되게 출력 전류에 영향을 준다.

1차 측 제어 (PSR)에 대한 분석 모델을 수립하기 위해서는 클램프 전압에 대한 공식도 필요하다. 참고 문헌 [2] 또한 편리하게 우리에게 그 해답을 제공하고 있다.

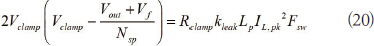
수식 (20)을 살펴보면, Vclamp 가 피크 전류 함수이기도 하다는 것을 알 수 있다. 또한 수식 (19)과 (20)은 모두 2 차 방정식으로, IL,pk  및 Vclamp 에 대한 기호식을 수작업으로 추출하려고 하면 오류 (가능성)가 있는 고엔트로피 결과를 초래할 수도 있다. 

이러한 매개 변수들의 값을 얻는 가장 간단한 방법은 매스캐드 (Mathcad® )와 같은 수학적 시뮬레이션 프로그램을 사용하여 두 등식에 의해 형성된 시스템을 해결하도록 요청하는 것이다. 일단 IL,pk 및 Vclamp 를 계산하면 출력 전류값도 추론할 수 있게 된다.

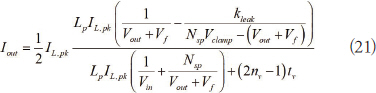
요약하면, PSR 플라이백 컨버터의 분석 모델은 세 등식 (19), (20), (21)을 해결하는 것으로 이루어진다. 수식 (21)을 사용하여 전류값을 얻기 위해서는 우선 수식 (19)로 피크 전류 IL,pk 를 계산해야 하다. 

그런 다음 입력 전압과 출력 부하 (LED 스트링은 출력 전압을 설정)에 의해 지정된 작동 설정값에 해당하는 수식 (20)을 이용해 클램프 전압 Vclamp 에 이르게 된다.

그림 7에서는 입력 전압이 120 V dc에서 375 V dc까지 변할 때 분석 모델로 얻어진 출력 전류를 매스캐드 (Mathcad® )를 사용하여 도식화했다. 출력 전류는 두 개의 서로 다른 출력 부하에 대해 그려진다.

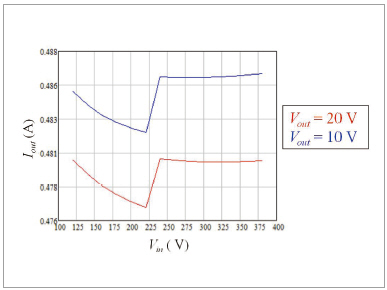
▲ 그림 7. 출력 전류 변화 대 입력 전압

-Vout = 20는 6 개의 직렬 LED를 나타낸다. 

-Vout = 10V는 3 개의 직렬LED를 나타낸다.

분석 모델의 정확성에 대해 어느 정도 확신을 얻기 위해 NCL30082로 제어되는 10-W LED 드라이버의 측정이 수행되었다. 그림 8은 10-W LED 드라이버의 회로도를 나타낸 것이다. 120 V 에서 375 V까지의 다양한 직류 전압이 보드 입력에 적용되었다. 출력 부하는 6 개의 LED (Vout = 20 V)에서 3 개의 LED (Vout = 10 V)까지 다양했다. 

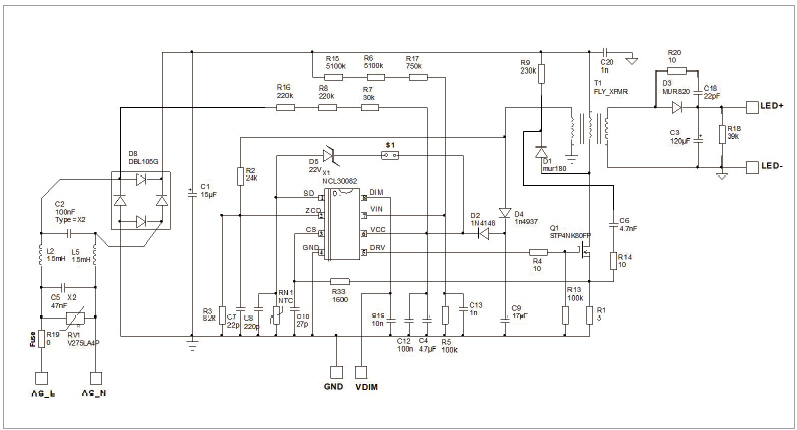
▲ 그림 8. NCL30082 평가 보드 회로도

그림9는 분석 모델로 얻은 출력 전류 변화와 LED 드라이버로부터 얻은 측정값들을 그래프로 나타낸 것이다. 이 샘플에 대한 출력 전류 변화가 꽤 잘 예측됨을 볼 수 있다. 분석 모델에 의해 예측된 평균 전류와 측정치 사이에 약 1 %의 오프셋이 있지만, 모델에 대표 값들만 입력했다. 실제로 보드의 모든 구성 부품은 해당 값에 대한 초기 허용 오차를 가진다. 

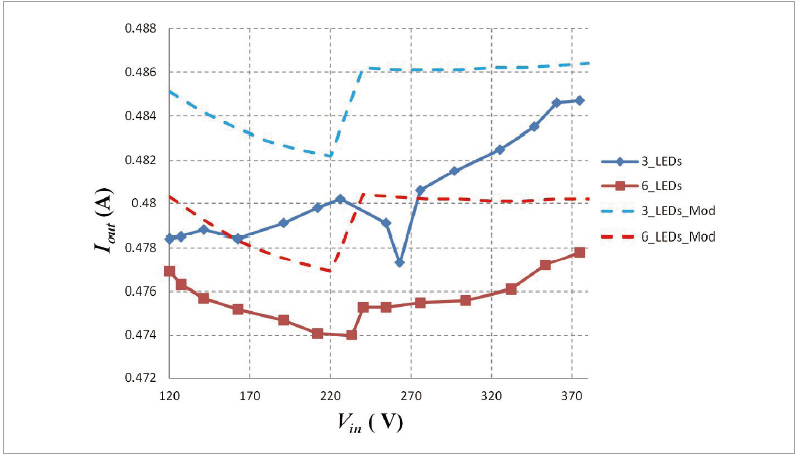
▲ 그림 9. 비교 분석 모델 대 측정값

또한 분석 모델은 출력 전류 설정치를 감소시키는 경향이 있는 2차 정류기 역회복 시간의 효과 (Secondary Rectifier Reverse Recovery Time) 를 고려하지 않는다.

본 논문의 1부에서는 1차 측 정전류 플라이백(Primary-Side Constant-Current Flyback)에 대한 분석 모델을 도출하였으며, 이에 대한 유효성은 실제 PSR 플라이백 컨버터의 측정치와 분석 모델에 의해 예측된 출력 전류의 직접적 대비를 통해 고려되었다.

현재 분석 모델에 대해 어느 정도 확신을 가지고 있기 때문에 본 논문의 다음 부분에서는 컨버터 최악 조건(worst case)의 정확도에 대한 추정치를 구하기 위해 모든 범위의 회로 값들을 적용할 것이다. 

스테파니 칸는테(Stéphanie Cannenterre) 애플리케이션 엔지니어, 온세미컨덕터